第六回の連載では湯本が確立したテスト手法であるIDAU法のテストプロセスを、ソースコードレベルのテストに応用した、Code Based IDAU法(CB-IDAU)について説明しました。第七回では、第５回の記事の中で述べたもう一つの応用研究の仮説の一つである、数学的グラフ特徴量によるバグ予測(Mathematical Graph Feature Metrics Test)の研究について説明したいと思います。(以降、本研究で提案するバグ予測モデルをGMTと表記します。)
GMTの仮説と目的
第五回の記事において記載した、湯本が確立したIDAU法をソースコードレベルのテストに応用したCB-IDAU法を実現するために必要になったデータや結果を応用した、GMTについて、再度、説明します。
IDAU法をソースコードレベルのテストに応用したCB-IDAU法を実現するために、テストのインプットデータとなるソースコードのデータを、一旦、Control Flow Graph (CFG)の数学的なグラフ構造に変換する必要がありました。そして、IDAU法に必要となるCRUDデータも、CFGのグラフノードに属性情報として付与することが必要でした。CB-IDAU法では、このCRUD情報が属性情報として付与された数学的グラフ構造であるCFGを、IDAU法のテスト抽出プロセスに従ってテストケースを抽出するために利用しましたが、他の用途として静的コードバグ予測のためのインプットデータとしての活用が仮説として考えられます。なぜなら、このCFGのデータ構造はソースコードの情報を数学的なグラフ構造としてモデル化されており、数学的グラフ特徴量やCRUD情報を静的コードのメトリクスとして、発生したバグとの相関性を計算することが出来ると考えられるからです。一般的によく知られている静的コードバグ予測のメトリクスとして、LOC、ネスト数、複雑度のようなメトリクスが知られていますが、数学的グラフ特徴量やIDAUで利用したCRUD情報をメトリクスとしてバグ予測が可能ではないかという仮説の元、実際に発生したバグ情報との相関性を計算し、バグ予測モデルを作成することが、GMTの目的なります。
図1にGMTのバグ予測モデル生成のためのプロセスのイメージを示します。
図1 GMTイメージ
仮説実現のための課題と対策
本研究では、既にCB-IDAU法を実装した時点で、ソースコードを中間コードに変換し、CRUD情報を属性情報として付与したCFGを網羅的に生成可能な状況ではあるものの、GMTの目的であるバグ予測モデルを作成するためには、以下の課題があります。
- 課題1. モデル式の定義
バグ予測を行うためには、各メトリクスとバグ情報との相関関係をモデル式として表現する必要があるが、具体的にどのようなモデル式を作成するのか？
- 課題2. 数学的グラフ特徴量の計算
すでに大量のCFGを生成する基盤を確立しているものの、これらの情報から具体的にどのようなアプローチで数学的グラフ特徴量を計算して保持するのか？また、どのような特徴量をバグとの相関を計算するメトリクス候補として採用すべきか？
- 課題3. バグ情報の取得
CFG上の特徴量と実際に発生したバグ情報との相関を調べるために、過去の大量のバグ情報を取得し、相関を計算可能なデータ形式として保持する必要があるが、具体的にどこから、どのような手法でバグ情報を取得し、どのようにデータを表現するべきか？
GMTの研究においては、これらの課題を克服するために以下のような対策を行いました。
- 課題1の対策：重回帰解析とAICの採用
バグ予測のモデル式としては、目的変数としてバグ情報、説明変数としてグラフ特徴量などの各メトリクス値として、離散型二項分布一般化線形モデル(Binomial General Liner Model)を採用しました。また、目的変数であるバグ情報との関連が最も深い説明変数を絞り込むための手法として、統計学の手法の一つである、AIC (Akaike Information Criterion)を用いました。重回帰分析の式は、目的変数Y、説明変数Xiとし、各説明変数の係数をαi 、補正項をβとし、iを１からnまでの整数値でメトリクスの総数を表すとすると以下の式で表現出来ます。
Y = α1X1 + α2X2 +・・・＋αnXn +β (式1)
本研究ではそれぞれの変数を以下のように定義し、バグ予測モデル式として用います。
Y : バグ情報
X : 既存の静的コードメトリクス値や数学的グラフ特徴量
α: 各メトリクスや特徴量がどれだけバグに相関しているかの重み係数
後述するバグ情報やメトリクス・特徴量の大量のデータから、代表的な統計解析ツールであるRのライブラリを利用して、重回帰解析とAICの計算を行うことで、最もバグYに相関のあるメトリクス・特徴量Xのセットを抽出し、その重み係数も付与します。
- 課題2の対策：igraphによる数学的グラフ特徴量の計算
CFGから数学的グラフ特徴量を計算するために、本研究ではRの代表的グラフ計算・可視化ライブラリであるigraphを利用しました。下図2にigraphを利用してBonachich Power 中心性の特徴量を計算し可視化したグラフを図示します。このグラフは、連載第五回にも掲載したグラフになります。
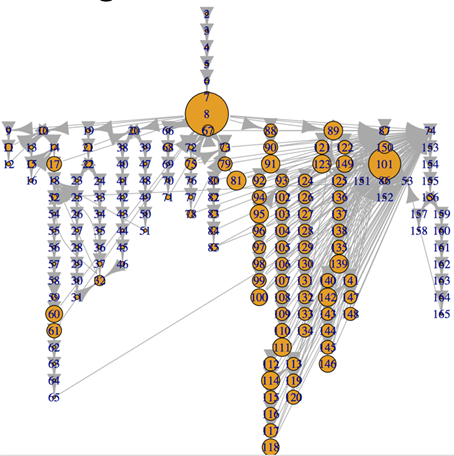
図2 igraphで計算したグラフ特徴量 Bonachich Power中心性の例
数学的グラフ特徴量の一つである中心性とは、グラフ全体の中でどれだけ多くのノードとの関係を持っているかの指標になります。Bonachich Power中心性は、特定のノードに対してより他ノードとの関連の多さをから強い影響力を持っているノードを示す、強者と弱者の関係を持つノードを表す指標になります。上記のグラフではNo8のノードとNo101のノードが特に大きな値を持っています。実際にどのような処理を担っているノードかを掘り下げて調べると、No8のノードは、パラメータのNullチェックを行う処理に関連するノードであり、No101は複数のメソッドを実行する処理に関連するノードになります。仮に、これらの処理に不具合があった場合、バグとして検出されていた可能性が考えられるため、Bonachich Power中心性の指標の高さはバグとの相関が高そうに見えます。しかし、これは、単に１例でしかなく、汎用的にこのような性質があるのかは、より多くのサンプルを検証して、その汎用性を検証する必要があります。そのため、本研究では以下に示す、3個の既存の静的コードメトリクスと、７個の数学的グラフ特徴量を説明変数の候補として採用しました。
表1 バグ予測モデル式の説明変数
| 既知の静的コードメトリクス | ||
| X1 | Code Steps | CFGに対応するソースのステップ数 |
| X2 | Complexity | CFGに体操するソースの複雑度 |
| CB-IDAU法で抽出したCRUD情報 | ||
| X3 | CRUD | CB-IDAUで付与した各ステップ毎のCRUD情報 |
| 数学的グラフ特徴量 | ||
| X4 | Edge Degree | CFGに含まれるエッジの総数 |
| X５ | Node Degree | CFGに含まれるノードの総数 |
| X６ | Eccentricity Centralization | グラフを円とみなした時に中心からの距離を指標とした離心中心性 |
| X7 | Eigenvector Centralization | 高次のノードと繋がる程度を表す固有ベクトル中心性 |
| X8 | PageRank | 固有ベクトル中心性にリンク流入性の概念を取り入れた中心性であり、Googleの検索アルゴリズムとして利用された指標 |
| X9 | Bonachich Power Centralization | 強者と弱者の関係を表す中心性 |
| X10 | Betweenness | あるノードが他のノード間の最短経路上にある頻度を示す中心性の指標 |
表1のX6からX10までの説明変数に、数学的グラフ特徴量の値が入ります。実際にあるCFGに対して其々の数学的グラフ特徴量を掲載して、値の大きさを各ノードの円の大きさとして可視化した場合の例を以下に示します。
図3 Betweenness
図4 Bonachich Power
図5 Eigenvector Centralization
図6 Eccentricity Centrality
図7 Page Rank
- 課題3の対策 : GitHubからのバグ情報の自動取得
上述した対策により説明変数の値については取得することが出来ますが、CFGに変換されたソースコードに対するバグ履歴の情報である目的変数Yをどのように取得するかが課題として残っています。本研究では各CFGに対応するバグ情報をGitHubのgit log情報をAPIから自動取得するスクリプトを実装することで、バグ情報を取得しました。また、１つのCFGはJavaであれば1メソッドの実装に対応するため、各メソッドのコードに対するバグ情報が存在していた場合にはY=1とし、存在しない場合にはY=0とする単純なBinominalの一般線形回帰モデルが適用出来るようにしました。
バグ予測モデル生成プロセス
GMTにおいてソースコードからバグ予測モデルを生成するまでのプロセスについて説明します。下図3には全体の４つのプロセスを図示しています。プロセスの１と２は、既に前回連載のCB-IDAU法にて説明したプロセスと同一であるため、主にプロセス3と4について詳細に記載します。
図8 GMTのバグ予測モデル生成プロセス
- プロセス1. 中間言語への変換
前回連載のCB-IDAU法と同様のプロセスであるため、前回連載の記載を参照下さい。
- プロセス2. CG作成
前回連載のCB-IDAU法と同様のプロセスであるため、前回連載の記載を参照下さい。
- プロセス3. 静的コードメトリクス・数学的グラフ特徴量の付与
前述の(式1)として定義したモデル式の各変数に取得した其々のデータを代入して重み係数であるαnを計算します。本研究で説明変数候補としてデータ取得した項目と、目的変数であるバグ情報を其々(式1)に対応させると、本研究で生成するBinomialの一般線形解析の式は以下のようになります。
図9 Binomial 一般線形回帰モデル
- プロセス4. AICによるバグ予測モデル式の生成
また、図４のモデル式は、候補となる説明変数を全て用いたモデル式になっていますが、この状態は仮説として候補となり得る説明変数で作成したモデル式になっているため、ここから、さらに精度を向上させるために、表1に示した10個説明変数の内、最もバグ予測の有無情報に相関が強い説明変数のセットを、AICを用いて絞り込みを行います。AICの詳細な説明は統計学の分野になるため省略しますが、本研究ではAICの計算にもRの関数を利用しました。図10にAICによる説明変数削減のイメージを図示します。
図10 AICによる説明変数削減イメージ
検証実験結果
本研究の検証用のテスト対象ソースコードは、代表的なオープンソースJavaアプリケーションサーバの一つであるTomcatのソースコードを利用しました。また、検証方法としては、GMTとして導出したバグ抽出モデル式と、既知の静的コードメトリクスのみを利用して導出したバグ抽出モデル式の２つのモデル式を導出し性能比較を行いました。こうすることで、GMTとして提案した新規のモデルが、既知のモデルよりどの程度の優劣があるか評価することが出来ます。性能指標としては、２値分類予測における一般的なモデル性能指標である、混合マトリックスを用いて、真陽性(TP)、偽陽性(FP)、真陰性(TN)、偽陰性(FN)、正確性(Accuracy)、精度・適合率(Precision)、再現率(Recall)を用いて評価を行いました。
- GMT：バグ予測モデル式の導出
下図11に実際のRを用いてGMTのバグ予測モデルを計算して導出した結果画面を図示します。図11では、表1に示した10個の説明変数を持つモデル式を作成した後に、AICを用いて、もっともバグの発生に相関がある5つの変数とされる、Edge-Degree, Node-Degree, Eccentricity-Centrality, Betweenness, Eigenvector-Centralization に絞り込みをおこなっています。
図11 GMTのAICによるモデル式導出結果
- 既存静的コードメトリクス：バグ予測モデル式の導出
下図12にGMTの比較モデルとして、既知の静的コードメトリクスである、表1に示した説明変数のX1(Step-Count)とX2(Complexity)のみを用いてバグを予測するモデル式をRのglm関数(一般化線形モデル)を利用して導出した結果を示します。
図12 既知の静的コードメトリクスを用いたバグ予測モデル式の導出
- 既存の静的コードメトリクスと数学的グラフ特徴量の比較結果
図11と図12の計算により、GMTのバグ予測モデル式と、既知の静的コードメトリクスを用いたバグ予測モデル式の２つの予測モデル式を得ることが出来ました。この２つのモデル式を利用して実際のソースコードからバグの有無を予測した場合、実際のバグ発生情報との乖離の具合を比較することで、GMTのバグ予測モデルが既存の静的コードメトリクスよりも、バグの存在有無を予測するのに有効性があるかを評価することが出来ます。評価の方法としては前述した通り、混合マトリクスの指標に従って性能評価をします。図13と図14にTP, FP, TN, FNの指標の違いを図示します。また、正確性(Accuracy)、精度・適合率(Precision)、再現率(Recall)も含めた各性能指標値の差異を表2に示します。
図13 GMTのバグ予測モデルの混合マトリックスイメージ
図14 既存の静的コードメトリクスによるバグ予測モデルの混合マトリクスイメージ
表2 混合マトリクスの各指標の差異
| Item | Our Model | Traditional Model | Difference (Our Model) – (Traditional Model) |
| TP Ratio | 0.64 | 0.66 | -0.02 |
| TN Ratio | 0.16 | 0.03 | +0.13 |
| FP Ratio | 0.13 | 0.25 | -0.12 |
| FN Ratio | 0.08 | 0.06 | +0.02 |
| Precision | 0.83 | 0.73 | +0.10 |
| Recall | 0.89 | 0.92 | -0.03 |
| Specificity | 0.56 | 0.12 | +0.44 |
| Accuracy | 0.80 | 0.69 | +0.21 |
- 評価結果
図14に示すように、既存の静的コードメトリクスでは大部分の予測結果が陽性と検出されており、どんなソースコードでもバグありと検出してしまう傾向があるのに対して、図13に示すとおりGMTのモデルでは、「真陰性(TN)」、つまりバグではないものをしっかりと検出しており、陽性・陰性の検出性能がバラついているためモデルとしての汎用性は高いと言えます。一方、陰性データも検出するトレードオフとして、「偽陰性(FN)」つまり間違ってバグ無しと判別する頻度が増えてしまっているため、改善の余地がまだあるのと、検証データのバリエーションを増やして検証する必要がありそうです。
まとめ
今回は、CB-IDAU法の研究において生成されたCFGのデータを流用して実施した派生研究であるGMTについて説明しました。既知の静的コードメトリクス値や、数学的グラフ特徴量データを付与した大量のCFGデータを用いて、実際のバグ発生データを教師データとして回帰分析を行うことで、GMTというバグ予測モデル式を生成しました。新規提案バグ予測モデルであるGMTの性能としては、既知の静的メトリクスよりもバグではない陰性コードの検出能力の向上が見られたものの、個々の性能指標を見ると、まだ改善が必要であることが分かりました。また、AICを用いてバグに相関の強い説明変数に絞り込みを行った結果としては、残った５つの説明変数全てが数学的なグラフ特徴量であったことから、さらにコミュニティ抽出などの異なる手法も合わせて用いることで、精度の向上も見込める可能性も考えらます。そして、大規模なデータと多くの特徴量によるモデル生成を試みることで、さらなる精度向上が見込めると思われます。次回は、湯本と武田で、これまでの連載の総括として、この研究の今後について対談を掲載します。
第1回：バージョンアップ開発や派生開発のときの影響範囲をテストしていますか？
第2回：バージョンアップ開発や派生開発のときの影響範囲をテストしていますか？
第3回：バージョンアップ開発や派生開発のときの影響範囲をテストしていますか？
第4回：バージョンアップ開発や派生開発のときの影響範囲をテストしていますか？
