
こんにちは、QAエンジニアのヒイロです。
情報処理に触れていると2進数、16進数という言葉を見聞きしたことがあると思います。
知識はあるけれど実際に触れたことのない方や、n進数そのものをこれまで知らなかったという方向けに、その注意点をn進数の中の2進数と16進数に焦点をあてて執筆しました。
はじめに
私がはじめてテスト業務に携わったのはオープン系のシステムでしたが、すぐに制御系に移行し、それ以降は日々16進数を取り扱うことになりました。
しかし、n進数に馴染みがなかったため、テスト設計から実行まで一貫して行った結果、NGになった項目はシステムの不具合ではなく「n進数について学習レベルの知識のまま設計していた」ことが原因で、設計自体に問題があったことがほとんどでした。
そこで、この記事では「気を付けるべきn進数のポイント」を紹介したいと思います。
n進数概要
10進数とは
私たちが普段使用している数え方です。
0~9の10個の数字を使用しているので10進数です。
2進数とは
2進数は0と1の2個の数字しか使用しないので2進数です。
「0と1しかないの?2とか3はどうなるの?」という疑問は表1を参照してください。

16進数とは
0~9, A~Fの16個の数字を使用するので16進数です。
A~Fはアルファベットですが数字として扱います。
※つまりn進数とは、n個の数字を使用して数を表す方法です。n進むと桁が繰り上がります。
2進数/16進数の存在理由
「なんでこんな面倒な数を使うの?分かりにくいなぁ」って思った方に説明します。
人間は両手の指の数を合わせて10になる数、10進数を扱うのが得意です。それと同じでコンピュータは0か1かの2つの数字で情報を扱うのが得意です。皆さんおなじみのフラグがわかりやすいと思います。ONは1、OFFは0という使い方がされますよね。
2は10、3は11、4は100というように、2進数では0と1以外は存在しません。けれど0と1だけで数字を表現すると桁がどんどん膨大になってしまうので、4桁毎の4ビットに区切って変換できる16進数が使われています。
【n進数が用いられている実例】
カラーコード、文字コード、デバイスIDなどで16進数が使用されています。
カラーコード
画像系アプリやhtml、CSSで色を指定するのには16進数のカラーコードが用いられています。
白色は#FFFFFF、黒色は#000000です。目にしたことがあるのではないでしょうか。
文字コード
テキストエディタなどで任意の1文字を範囲選択などするとステータスバーなどに表示されるものもあります。
たとえばS=53 c=63 r=72 i=69 p=70 t=74 s=73でScriptsは53637269707473となります。
※Sとsの違いで分かるように、大文字と小文字ではコードが異なります。
MACアドレス
ネットワーク搭載機器(ルーター、PC、スマホ等)にも先述の0~9, A~Fの16進数が使われています。
デバイスマネージャ
windowsのデバイスマネージャからデバイスの詳細を確認するとハードウェアIDに16進数が表示されます。
【業務での使用例】
Web系ではあまり馴染みがないですが、組み込み系や制御系のテストで扱う場合があります。特にCAN通信[※1]では必須となります。
私は電子部品の状態確認や制御、ログ解析等に16進数を用いました。とある案件では各種仕様書、設計書、マニュアル等からテスト設計もすべて16進数表記でした。一般ユーザ向けのスマホアプリで、機器の送信する値をPCで受信しながら動作確認するという事例もあります。
[※1] CAN通信:自動車などの機械に用いられる通信規格。部品同士の情報を送受信するもの。
「見たことあるかも!暗号みたいなものだと思ってた」という方もいるのではないでしょうか。暗号ではなく、ちゃんと意味のある数字(とアルファベット)なのです。
【n進数の変換】
ではその暗号のような数字をどう解読したら良いのでしょうか。
ぱっと見て頭の中で変換できる方はそうそういないと思うので、次のような計算が必要になります。
Windows標準の電卓
設定を「標準」から「プログラマー」というモードに切り替えます。DEC,BIN,HEX,OCTという略称が並んでいますがDECが10進数です。
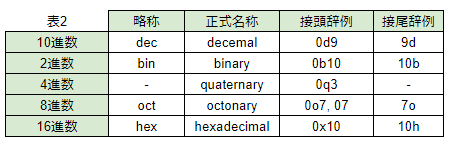
DECに任意の数字を入力すると、それぞれに対応する値が瞬時に表示されます(略称については表2参照)
(※4進数のみ非対応)
表計算の関数
例として10進数から変換する場合は=DEC2BIN,=DEC2HEX,=DEC2OCTを用います。
10進数の11を2進数にしたい場合は「=DEC2BIN(11)」とすると1011に変換されます。
2,8,16進数から変換したい場合はDECをBIN,OCT,HEXに入れ替えます。
(※4進数のみ非対応)
表1から割り出す
例として[0000 0111 1110 1000]という2進数を16進数に変換する場合
表1で0000=0, 0111=7, 1110=E, 1000=8と分かるので、結合して16進数は[07 E8]です。
(※4,8進数も同じ方法で変換可能)
n進数取り扱い注意点
接頭辞の罠
先述の表2について「数字の前の0dとかhとかって何?見づらいよ!」と思いませんか? 私は最初の頃思っていました。これは接頭辞と呼ばれるものです(接尾辞になる場合もあります)。
10進数しか扱わない現場であれば[ 100 ]と言えば[ 0d100 ]のことですが[ 0d77 ]、[ 0d99 ]のようにすべての値に[ 0d ]などと記載するのは確かに面倒だし邪魔です。
ですが他のn進数を取り扱う現場では何進数なのかがハッキリしないと、2進数の[ 100 ]は10進数だと4、16進数の[ 100 ]は10進数では256となり、まったく異なった値となります。
【テスト設計例1】
あなたは温度を示すアプリのテスト設計をすることになりました。詳細設計書には下記の記載があります。
「項目Aの値を1/2し、その結果でフォント色を下記のようにする。
・100以上:赤、51以上:オレンジ、それ以外:青色」
項目Aを確認すると値は[ 110 ]でした。そこであなたは「110÷2で55だから…期待値はオレンジ色ね」とテスト設計しました。
ところが…
case1.
項目Aは2進数表記でした!(0b110だったのです)
表1を参照(または電卓のBINをクリックし[110]を入力)してください。2進数の110(0b110)は10進数では6(0d6)ですね。1/2すると0d3。つまり3度なので青色が正解でした。
case2.
項目Aは16進数表記でした!(0x110だったのです)
電卓でHEXに110を入力するとDECは272と表示されますね。1/2すると0d136。つまり136度なので赤色が正解でした。
接頭辞(接尾辞)の違いで同じ[ 110 ]でもここまで値に差が出てしまうのです。
エンディアンの罠
エンディアンの罠…16進数でのバイト順「byte order[※2]」のことで、下記3種類が存在します(なぜ1種類に統一されていないのかというと、所説あるようです)。
[※2] byte order:データは1byte(8bit)単位で記憶されるため、2byte以上の時に先頭からor末尾からのどちらから記憶していくかという順番。
ビッグエンディアン
バイナリデータの先頭が頭になる方式。主な用途:TCP/IPプロトコルや、UNIX、モトローラ、Macintosh等。
例えば[ 0d1234 ]を電卓で変換するとHEXは[ 4D2 ]と表示されます。1バイト目が[ 04 ]、2バイト目が[ D2 ]で[ 0x04D2 ]です。
リトルエンディアン
バイナリデータの末尾が頭になる方式。主な用途:Windows、USB、IntelやAMDのプロセッサ等。
先程の[ 0d1234 ]の場合、末尾からバイトをひっくり返した並びになるので[ 0xD204 ]になります。1バイト目が[ D2 ]、2バイト目が[ 04 ]ですね。
※単純に末尾から数字を逆順にして02D4や2D40としないようにご注意を。私は最初の頃間違えました…)。
バイエンディアン
ビッグ、リトルのどちらにもなる方式。主な用途:MIPS、ARMのCPU等。
10進数を4バイトの16進数にした時にbyte orderでどのような違いがあるかを表3に記載しました。
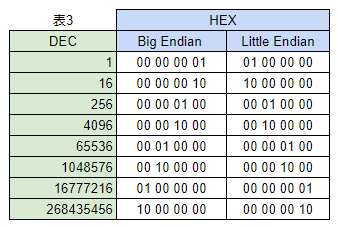
[ 00 00 00 01 ]はビッグエンディアンは0d1ですが、リトルエンディアンでは0d16777216です。10進数で考えると1と16777216では大きな差異になってしまいますね。
【テスト設計例2】
あなたは温度を示すアプリのテスト設計をすることになりました。詳細設計書には下記の記載があります。
「項目Bの16進数を10進数に変換したとき、その結果でフォント色を下記のようにする。
・5000度以上であれば赤色、それ以外は青色とする」
項目Bの値は[ 0x121A ]でした。
16進数であることが判明しているので[ 0x121A ]を電卓で変換すると[ 0d4634 ]でした。
「4634度ね。5000度以上ではないから…期待値は青色ね!」
ところが、項目Bはリトルエンディアン表記でした。リトルエンディアンで[ 0x121A ]はビッグエンディアンにすると[ 0x1A12 ]で、変換すると[ 0d6674 ]。つまり6674度なので5000度以上となるため赤色が正解でした。
「全項目ビッグエンディアンで期待値算出してたよ…計算しなおさないと」ってことにならないように、私は16進数を見かけたら「ビッグエンディアンですか?リトルエンディアンですか?」と必ず設計前に確認するようにしています。
※ちなみにエンディアンとは「ガリバー旅行記」で卵を尖った小さい方から食べる(little end)か、大きい方(big end)から食べるかで戦争をしている国のエピソードからきているそうです。「こしあんか粒あんか」「頭からかしっぽからか」「タケノコかキノコか」みたいなものですね
小数点の罠1
[ 0xA.B ]と記載があった場合、[ 0xA. ]はそのまま[ 0d10. ]です。
「Bは10進数では11だから…0d10.11ね!」となりがちですが…16進数では0.1の位は1/16、0.01の位は1/256なので、0xBを10進数に変換(0d11)し、それを16で割ってください。11/16=0.6875で、正解は[ 0d10.6875 ]となります。
n進数で小数点以下の変換ができるサイトや、小数点第2位以下の計算についても記事がたくさんあるので興味のある方は是非調べてみてください。
小数点の罠2
現場や設計、プログラマにより小数点以下の扱いは四捨五入、切り捨て、切り上げなど仕様がさまざまです。
表4をご覧ください。B列は単純に0d100をA列の値で除算(=100/1 ~ =100/16)した値です。

C列はB列の値をround関数で四捨五入した値。
D列はC列の値を「=DEC2HEX(decemal→hexadecimal)」という関数で変換した16進数です。
E列はB列の値を「=DEC2HEX」で変換した16進数です。
赤背景の行は値が変わってしまいました。
【テスト設計例3】
温度を示すアプリのテスト設計をすることになりました。
詳細設計書には「項目Cの温度を1/2した値を16進数に変換し、項目Dの値とする」と記載されています。項目Cの値は[ 135度 ]です。
[ 0d135 / 2 ]は[ 0d67.5 ]ですね。
[ 0d67.5 ]を[ =DEC2HEX(67.5) ]すると[ 0x43 ]でした。
「じゃあ項目Dは [ 0x43 ]ね!」とテスト設計しました。
ところが…
項目Dは四捨五入で求める必要がありました。DEC2HEXという関数は小数点以下切り捨ての仕様となっています。
四捨五入や切り上げが必要な場合、round関数またはroundup関数をかませた後にDEC2HEXする必要があります。
この場合ですと次の手順になります。
- 135 / 2 = 67.5 を求める
- =round(67.5)で四捨五入し68にする
- =dec2hex(68)で16進数に変換し[ 0x44 ]を求める
つまり項目Dは[ 0x43 ] ではなく [ 0x44 ]が正解でした。
「全項目切り捨てで期待値出してたよ…算出しなおさないと」ってことにならないように、私は小数を見かけたら「四捨五入ですか?切り捨て/切り上げですか?」と必ず設計前に確認するようにしています。
まとめ
以上が私がn進数を扱うときに注意しているポイントの紹介でした。
どんなことでも「学習レベルの知識」があっても「実務でやってみたら思っていたのと違った」とか「あの時勉強したのはこういうことだったのか!」という気づきがあると思います。もしこの先n進数を扱うことになったら「そういうえば昔、記事で読んだな…」と思い出してみてください。
この記事がこれからn進数を扱うみなさんのお役にたつことがあれば幸いです。














