
帰納的な推論と発見的な推論(アブダクション)は、
私たちがソフトウェア開発の現場/実務で(知らず知らずにでも)駆使している思考の形です(それどころか日々の暮らしでも使っています)。
それほど“自然な”思考の形ですが、どんな考え方で、どんなところに注意すると質の高い思考ができるのか、基本知識を押さえておくと実務のレベルアップにつながります。
<実務三年目からの発見力と仮説力 記事一覧>※クリックで開きます
今回からは、“非演繹的”なもうひとつの推論、アブダクションの考え方を見ていきます。
今回は「仮説(説明仮説)って何?」「アブダクションって何!?」という話です。
ところで仮説って何だろう?
“なぜ” “どのように”を解き明かしたい、説明したい・して欲しい
帰納的推論で一般的な傾向を見つけたり、原因と結果の関係を見つけるのに加えて、
「その条件(原因)からなぜこの事象が起こるか」「原因から結果まで、どのようにして (どのような過程・機序で)起こるか」の説明ができれば、
推測の説得力は相当高まるでしょう。
アブダクションが考える仮説は、 このような「事象の原因を見つけたり、原因から結果に至る過程などを説明する」仮説(説明仮説)です。
よい仮説の性質
はじめに、当てずっぽうや思いつきの推測と一線を画す「よい仮説」が具えているべき性質を確認しておきましょう。
(参考:『論理学入門』)
いくつか考えられますが、外せないのは次の4点です。

- 問題となっている事象や因果関係を説明できる。
- 直接的/間接的に 真偽を検証可能(verifiable)である。
仮説自体でなくとも仮説がもたらす帰結などの真偽を、事実に照らして判断できる。
(反証可能性(偽であると検証できる)は、 誤った仮説を除外できるために重要な性質) - 説明能力が同じなら、より単純な仮説が望ましい。
複数の仮説が考えられて、同じように不整合や破綻がなく、同じように説明できるなら、単純な仮説を採るのがよい。 - 少数の仮定から、整合的に説明できる仮説が望ましい。
既に確立された知識・理解に基づいて、多くの仮定を足すことなく、系統的・体系的に説明できるのが理想的。
アブダクションとは
仮説を考える推論とその形式
19世紀から20世紀アメリカの哲学者・論理学者パースは、説明仮説の重要性と、よい仮説を考える推論(アブダクション)はどのようなものか(どうあるべきか)を研究しました。
パースによれば、アブダクションの典型的な形は次のように示されます。
(出典:『アブダクション 仮説と発見の論理』。太字は引用者による)
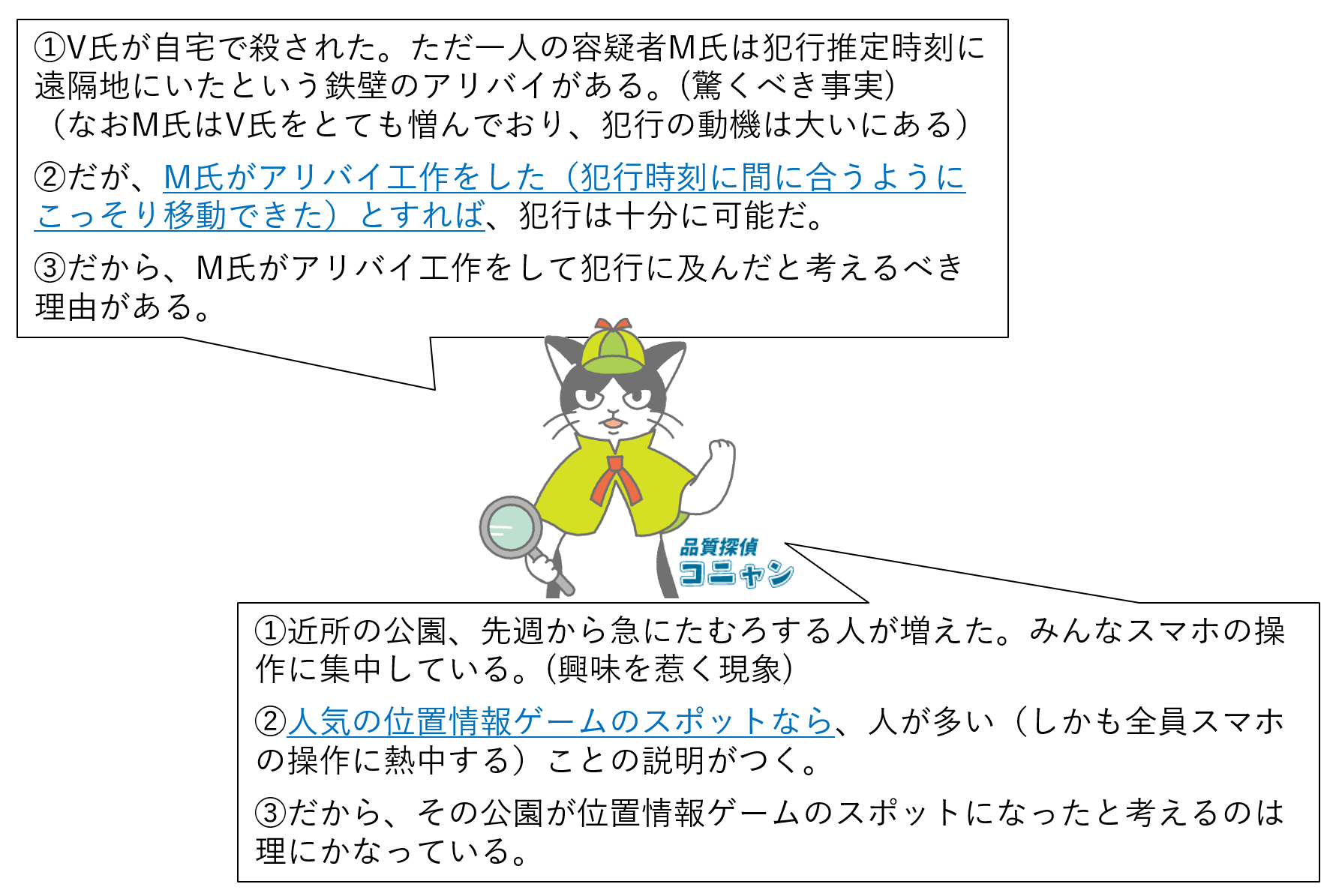
①驚くべき事実Cが観察される。
②しかし もしHが真であれば、Cは当然の事柄 であろう。
③よって、Hが真であると考えるべき理由がある。
「驚くべき事実C」とは、理由や原因を探りたくなるようなものごとや、解明が必要なものごとです。
(推理小説や推理ドラマの「不可解な事件」や、日常で「これは何だろう?」と不思議に思う出来事もそうです)
このCに対して「こう考えれば C は説明できる」と、“謎”の解消を図るのが仮説Hです(図6-1)。
アブダクションの形式面での特徴
図6-1の推論の形を図式化すると図6-2のようになります。
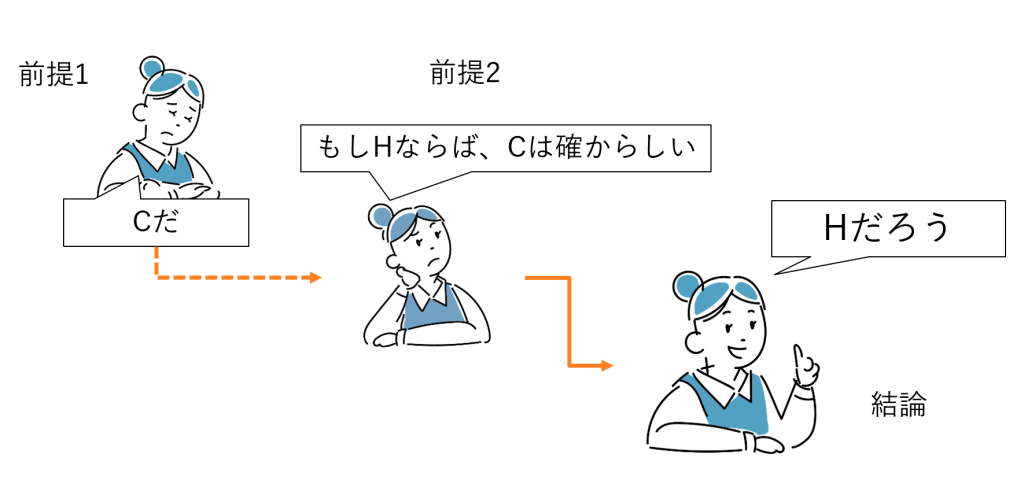
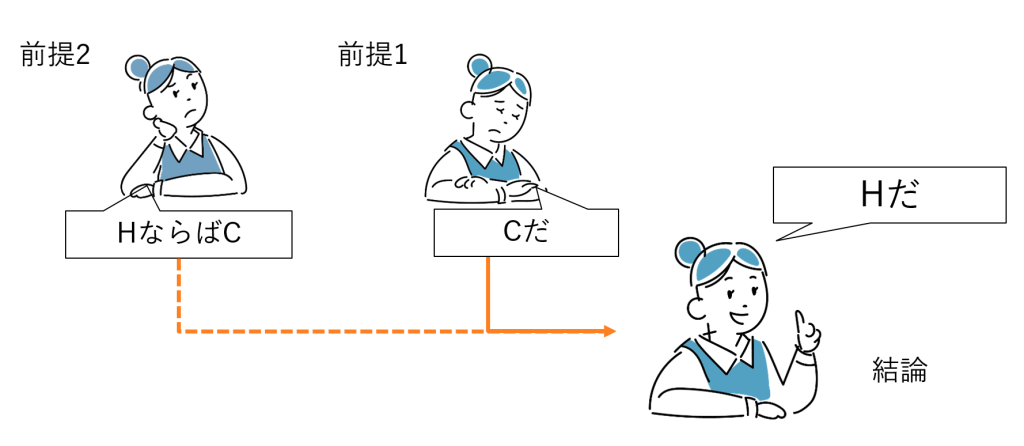
図6-2の前提1と前提2の順序を入れ替えると、混合仮言三段論法の形をしています(図6-3)。
つまり、アブダクションによる推論は、見かけ上演繹的な推論っぽい形をまとっています。
ただし、それは後件肯定という、演繹的な推論では誤りになる形です(図6-4。実践編「“ならば”を使って推論する」参照)。
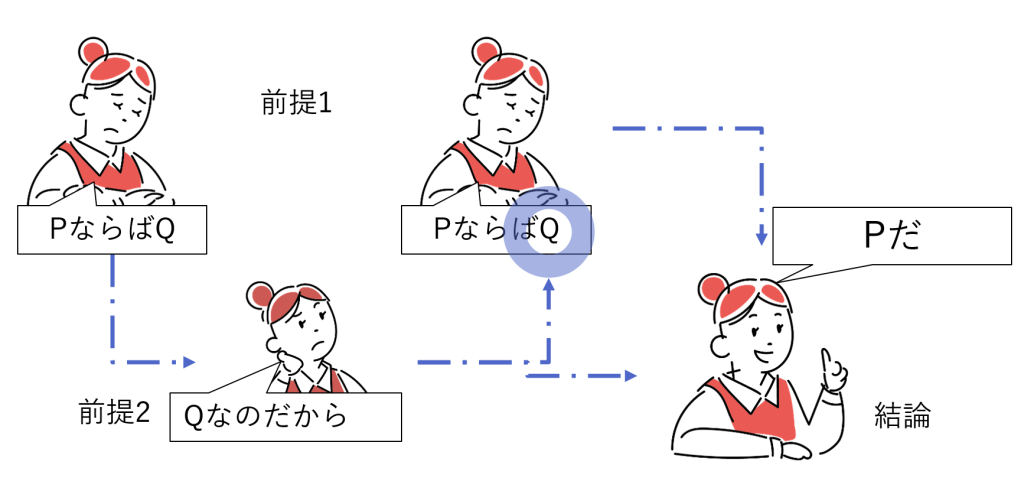
このように、
- (後件肯定という演繹的には誤った形ではあるが)後件(事実や結果)から、その後件を導く前件(前提や原因など)を“逆向きに”考え、
- 「そう考えるのが理にかなっている、もっともらしい」という説明仮説を発案する
のが、アブダクションという推論形式の特徴です。

ポリアの「発見的三段論法」
仮説を考える推論の、もうひとつの見方
続きを読むにはログインが必要です。
ご利用は無料ですので、ぜひご登録ください。














