[第6回] 文レベルのロジック (2)条件・場合を表す言葉

テストエンジニアが身につけておきたいスキルの一つに「論理スキル」があります。

この連載では、「プログラムのレベル」「文や文章のレベル」に分けて、論理スキルの基本である「論理の言葉」を徹底解説します。

＜テストエンジニアのための論理スキル[再]入門　連載一覧＞※クリックで開きます

[第1回] なぜ、テストエンジニアに(も)論理のスキルは重要なのか【連載初回、全文公開中】
[第2回] プログラムレベルのロジック (1)概要編
 [第3回] プログラムレベルのロジック (2)解説編・基本の論理演算
 [第4回] プログラムレベルのロジック (3)解説編・論理演算の組合せ
 [第5回] 文レベルのロジック (1)文レベルのAND/OR/NOT

第6回のテーマは、「文レベルの論理の言葉」のうち条件や場合を示す言葉の意味と働きです。

「希望者が5人集まったら、イベントを開催します」といった、

“特定の条件/場合を前提とした主張”を言いたい時があります。このような表現はソフトウェアにとっても重要であることは第1回で述べました。実際、ここまでに出てきた例の殆どで使われています（読み返してみてください！）。

この、条件や場合を示す言葉に出逢った時は、どういうことに注意を向けるとよいでしょうか。

前回に引き続き、一般的な文章や日常会話などで用いられる語句や表現を 一般語と呼びます。

条件・場合を表す言葉の基本形・“ならば”
逆・裏・対偶
- 「PならばQ」の“変形”
- もとの文と逆・裏・対偶との関係
条件・場合の表現をチェックする
- 具体例①
- 具体例②
むすび
参考文献

条件・場合を表す言葉の基本形・“ならば”

文章の中で“条件や場合を示す”際に目印として使われる語句の代表格が、“ならば”や“場合”です。

「論理の言葉」としての“ならば”

典型的な条件の表し方は、「PならばQ」という形を取ります。

「テストが全件合格したら、テストを終了する」
「当日雨天の場合、大会を中止とする」　etc.

Pを前提(仮定)または前件、Qを帰結または後件といいます。

「テストが全件合格」「当日雨天」が前提
「テストを終了する」「大会を中止とする」が帰結

「PならばQ」は、「Pという前提が成り立つなら、Qという帰結が成り立つ」ということを表しています。

この“ならば”の働きを「条件法」といいます（「もし昨日晴れていたら、○○ランドに行ったのに」のような、事実に反することを述べる条件法とは異なります）。

PとQの関係に注意してください。

「PならばQ」は、「Pが成り立つ時はQが成り立つ」「Pが成り立つのにQが成り立たないことはない」とだけ言っており、「Pが成り立たない時」のことは何も言っていません。

従って、PでなくてもQであることがあり得ます。（集合のベン図的に表すと、「PならばQ」は図6-1の左を指しています）。

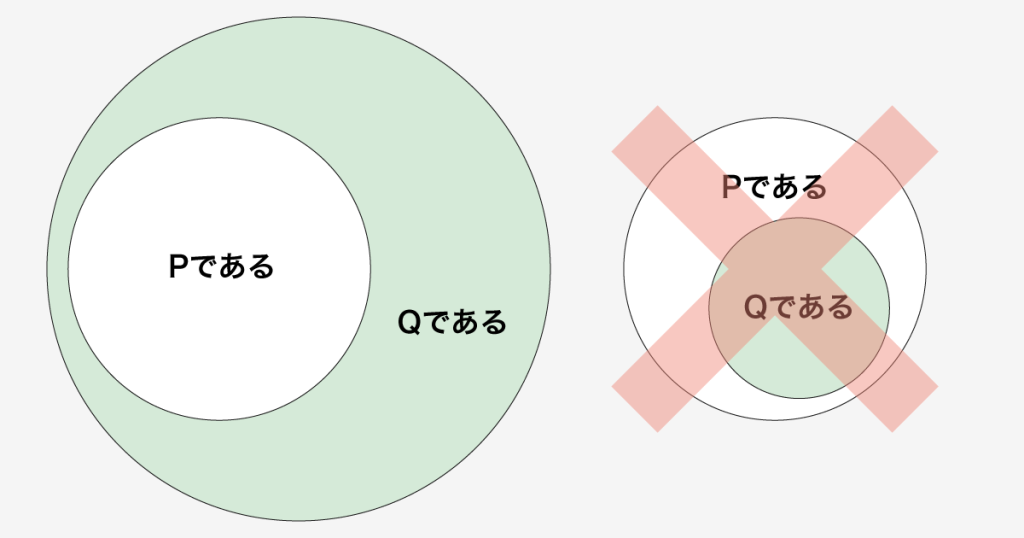
「テストが全件合格」していなくても、テストが終了することはあり得る（他の条件があるかも知れない）
「当日雨天」の他にも大会を中止する条件はあり得る（強風の場合、参加者が揃わない場合、など）

等値(同値)の“ならば”

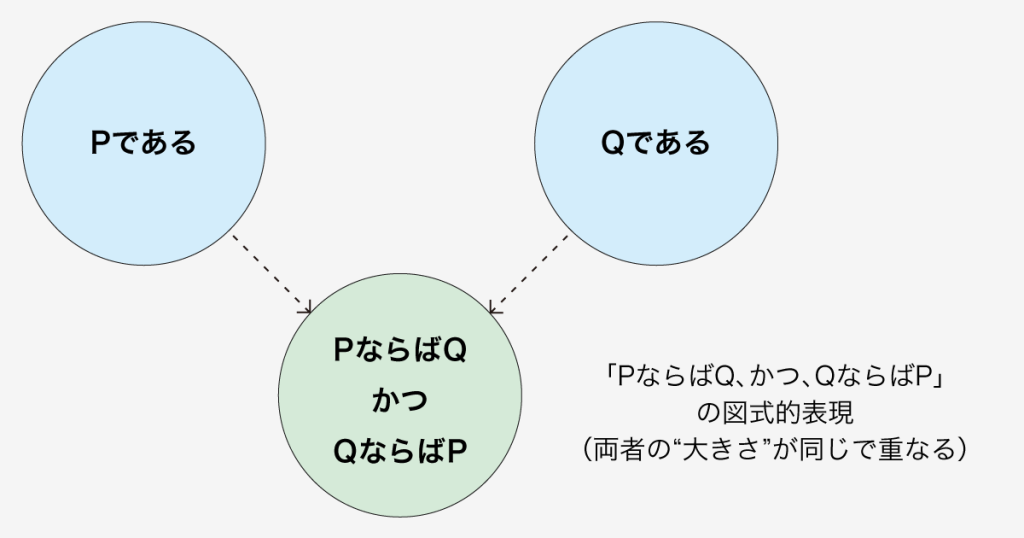
「PならばQ」もその逆「QならばP」もともに成り立つ、という場合もあり、これを「双条件法」といいます。（PとQが“同じ大きさ”でぴったり重なる。図6-2）

「稼働中にバッテリー残量が10%を切ったら、“充電して！”と音声で知らせます」
- 稼働中に“充電して！”と音声が流れる場合は、バッテリー残量が10%を切っている
「獲得ポイントが○○になったら、ランクAAになります」
- ランクAAになる条件は○○ポイント獲得のみ

等値(同値)の“ならば”を明示する語句として、「……の場合、そしてその場合に限り、～である」という言い回しが用いられることもあります。

（英語の論文などでは”if and only if …”という表現が使われます(“iff”と略される)）

ソフトウェアに出てくる“ならば”

ソフトウェアでは、条件や場合を示す“ならば”は、成り立つ成り立たないというよりは、特定の条件/場合に対応する特定の処理/動作や、特定の処理/動作ができるための条件を記述する局面で使われることが多いでしょう。

「条件を満たさない時の動作」といった記述が添えられることも多いです。

ある箇所で次のような記述があったとして：

「利用者がログインしており、SP権限を持っている場合は、XYZ機能を使うことができる」
「数値のいずれかがゼロの場合、エラーメッセージE1を出力する」

別の箇所で、

「別の条件が満たされている場合、XYZ機能を使える」や
「別の条件に該当する場合、エラーメッセージE1を出力する」

という記述があることもあります。

逆・裏・対偶

「PならばQ」の“変形”

「PならばQ」のP(前提)とQ(帰結)との関係に着目して、次の三種類の変形が考えられます。（図6-3）

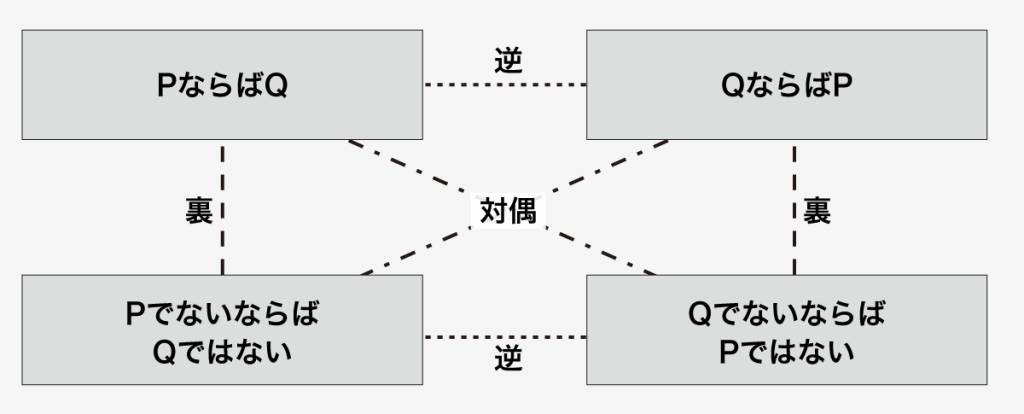
逆：　PとQを入れ替える。「QならばP」
裏：　PとQをそれぞれ否定する。
「NOT(P) ならば NOT(Q)」＝「PでないならばQでない」
対偶：PとQをそれぞれ否定し、さらに入れ替える
「NOT(Q) ならば NOT(P)」＝ 「QでないならばPでない」
- もとの文の「裏の逆(または逆の裏)」に等しい

逆・裏・対偶は、同じ変形を二度繰り返すと、もとの形に戻ります。図で確認しましょう。

もとの文：「PならばQ」
逆「QならばP」の逆は、「PならばQ」
裏「PでないならばQでない」の裏は、「PならばQ」
対偶「QでないならばPでない」の対偶は、「PならばQ」

なお、逆と裏は互いに対偶の関係にあります。（図6-3）

もとの文と逆・裏・対偶との関係

もとの文に対して、逆・裏・対偶について以下のことが言えます。

逆・・・「PならばQ」が成り立っていても、逆「QならばP」が成り立つとは限らない
- 「テストを終了するなら、テストが全件合格している」？？
- 「大会が中止になるなら、当日雨が降っている」？？
- （「等値(同値)の“ならば”」なら、逆は成り立つ）
裏・・・「PならばQ」が成り立っていても、裏「PでないならばQでない」が成り立つとは限らない
- 「テストが全件合格していないなら、テストを終了しない」？？
- 「当日雨が降らないなら、大会は中止にならない」？？
- （「等値(同値)の“ならば”」なら、裏は成り立つ）
対偶・・・「PならばQ」が成り立つなら、対偶「QでないならばPでない」は必ず成り立つ
- 「テストが終了していないなら、テストが全件合格しているのではない」
- 「大会が中止にならないなら、当日雨は降っていない」

条件・場合の表現をチェックする

文章の理解を確実にするために、条件・場合の表現の逆や裏を考えて、文章全体を調べてみたり考えてみたりする方法があります。

逆：「Qが成り立つ場合には、Pという前提が成り立っていると考えてよいか」と考えてみる
裏：「Pでないならば、Qにはならないか」と考えてみる

具体例①

もとの文：「利用者がログインしており、SP権限を持っている場合は、XYZ機能を使うことができる」

逆：「XYZ機能を使うことができる」なら、「ログインしており、SP権限を持っている」と言えるか。他の場合はないか
裏：「ログインしており、SP権限を持っている」のでないならば、「XYZ機能を使う」ことはできないか

具体例②

もとの文：「数値のいずれかがゼロの場合、エラーメッセージE1を出力する」

逆：「エラーメッセージE1を出力する」ならば、「数値のいずれかがゼロ」であると言えるか。他の場合はないか
裏：「数値のいずれかがゼロ」でないならば、「エラーメッセージE1を出力」しないか

「同じ処理をする他の場合はないか？」「ここに記されている“条件や場合”を満たしていない場合の動作はどうなる？」といったことを自然に気にかけている人も多いと思います。それは、「PならばQ」の形の文に対して、PとQの関係が自然に気になるからなのかも知れません。

むすび

6回にわたって、“論理的”に考えるための「基本的な道具」である「論理(ロジック)の言葉」をいくつか見てきました。

取り上げたのはあくまでも「基本的な道具」です。これらを憶えたら、ぜひ次のステップに進んで論理のスキルを高めてください。

文章レベルの論理：文章の構造を理解するための論理の言葉
- 長い文章の筋道を追ったり、話を整理して論旨を把握するのに役立ちます
推論：考えの筋道を立てるためのルール
- 前提から結論を導き出したり、
  複数の事象を一般化して考えたり、事象から原因の仮説を立てたりする方法
  （故障の要因の推測や、故障の原因の推測などに役立ちます）

参考文献

『入門！論理学』(野矢茂樹 / 中央公論新社)
『論理的思考の技法〈1〉第2版　「ならば」をめぐって』(鈴木美佐子 / 法学書院)
『新版　論理トレーニング』(野矢茂樹 / 産業図書)
『スマリヤン先生のブール代数入門』(スマリヤン / 共立出版)
『記号論理学　一般化と記号化』(スマリヤン / 丸善出版)