[第3回] プログラムレベルのロジック (2)解説編・基本の論理演算

テストエンジニアが身につけておきたいスキルの一つに「論理スキル」があります。

この連載では、「プログラムのレベル」「文や文章のレベル」に分けて、論理スキルの基本である「論理の言葉」を徹底解説します。

筆者のnoteサイトで、「論理スキル[再]入門」を書こうと思った理由・経緯を綴っています。
■論理スキル・“入門編”のこと　(T3:Pt1:Ch01)
よろしかったらご覧ください。

第3回は、基本の論理演算・否定(NOT)、論理積(AND)、論理和(OR)の意味と働きを見ていきます。

各論理演算は、名前だけ見るとものすごそうに見えるかも知れませんが、ひとつひとつはそう難しい演算ではありません。まず、それぞれが「どういうことを言っているのか」を把握しましょう。日常でも同じような考え方をしている時がある筈です。

文中で「条件や主張」という表現を使っていますが、それはこれらの論理演算が文や文章のレベルでも使われるからです（第5回に記載予定）。

＜テストエンジニアのための論理スキル[再]入門　連載一覧＞※クリックで開きます

[第1回] なぜ、テストエンジニアに(も)論理のスキルは重要なのか【連載初回、全文公開中】
[第2回] プログラムレベルのロジック (1)概要編
 [第3回] プログラムレベルのロジック (2)解説編・基本の論理演算
 [第4回] プログラムレベルのロジック (3)解説編・論理演算の組合せ
 [第5回] 文レベルのロジック (1)文レベルのAND/OR/NOT

否定(NOT)
論理積(AND)
- 論理積(AND)とは
- 演算対象が三つ以上の場合
論理和(OR)
- 論理和(OR)とは
- 演算対象が三つ以上の場合
論理演算で表す例
むすび
参考文献

否定(NOT)

否定(NOT)とは

否定(NOT)は次のような演算です。

条件や主張の真理値を反転する単項演算(演算対象がひとつの演算)
- 否定の演算式を、本記事ではNOT(A)と表す
条件や主張Aが真ならNOT(A)は偽になり、Aが偽ならNOT(A)は真になる
日本語では、「Aではない」、「Aであるということはない」という語句が相当する

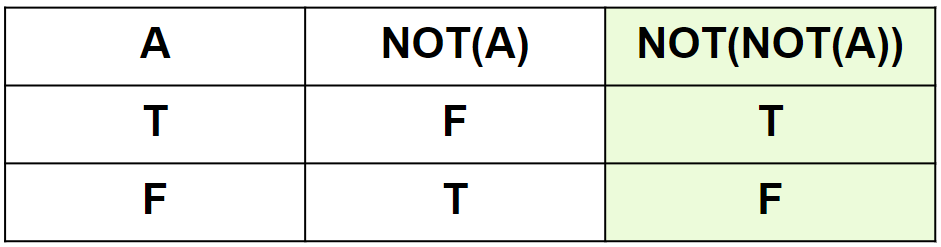
否定の真理値表を図3-1に示します。真理値表(真理表、真偽表とも)とは、演算対象の真理値と演算結果の真理値をまとめた表で、”T”は真(true)、”F”は偽(false)の意味です。以下の通りであることを確認してください。

Aが真の時、NOT(A)は偽になる
Aが偽の時、NOT(A)は真になる

二重否定

二重否定(否定の否定)は、もとの真理値と同じ値になります（もとの真理値に戻る）。（図3-2）

Aが真の時、NOT(NOT(A))は真
Aが偽の時、NOT(NOT(A))は偽

否定の留意点

否定そのものではありませんが、数値の範囲を表す表現の否定は、以下のようになります。（図3-3）

「以上」の否定は、“以上で(は)ない”＝“より小さい”＝「未満」
- 「xが10以上(x >= 10)」という条件式の否定は「x < 10」
「以下」の否定は、“以下で(は)ない”＝“より大きい”＝「超」
- 「yが50以下(y <= 50)」という条件式の否定は「y > 50」
上記の逆で、未満の否定は「以上」、超の否定は「以下」。
「超」という語はあまり日常会話的ではないが、ソフトウェアではよく使われる
日常で使う場合は、この辺りの大小・含む含まないの関係を“曖昧に”表し/解釈することがままあります。（第5回に記載予定）
日常で使う時の「否定」の、論理の言葉としての意味合いとの違いも、第5回で取り上げます

論理積(AND)

論理積(AND)とは

論理積(AND)は次のような演算です。

条件や主張A, Bがともに真である時に結果が真、そうでない場合には結果が偽になる二項演算(演算対象がふたつの演算)
- 論理積の演算式を、本記事ではA AND Bと表す
「ふたつの条件が同時に成り立つ(必要がある)場合」「ふたつの条件がともに必要である場合」などを表すのに用いる
日本語では、「および」「かつ」「ならびに」「そして」などの接続語が相当する
- 「そして」は時間的順序を表す意味もあるので注意が必要です

論理積の真理値表を図3-4に示します。

表の1行目が「A, Bがともに真の時」
2～4行目が「そうでない(A, Bがともに真、ではない)場合」
- “A, Bどちらかが偽”である場合を含む

演算対象が三つ以上の場合

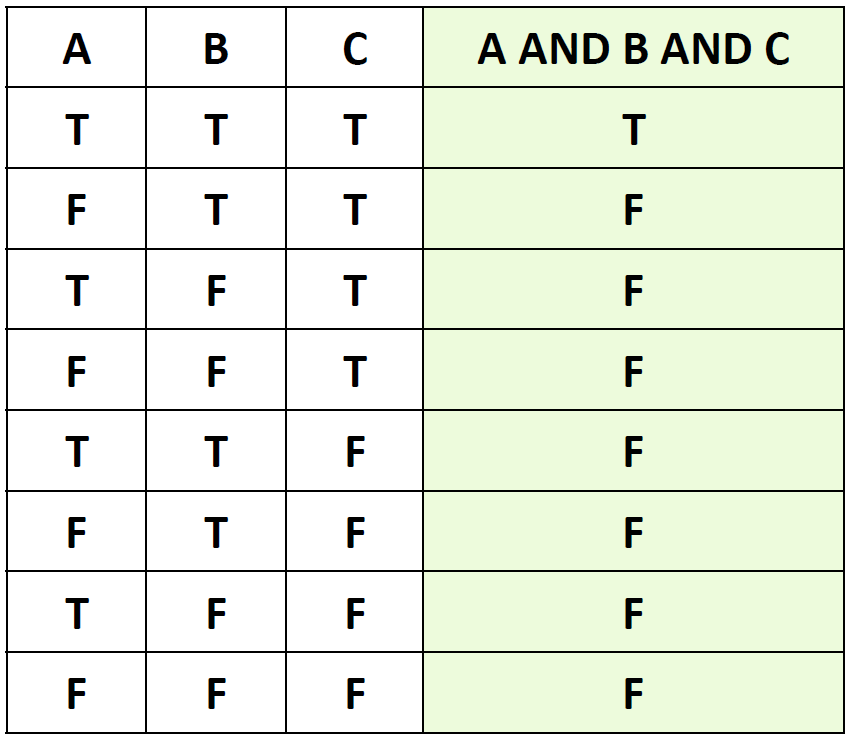
論理積は二項演算ですが、演算対象が三個以上になっても同じように考えることができます。（三条件の論理積の真理値表は図3-5参照）

演算対象がすべて真の時、結果が真
そうでない場合(＝どれかひとつ以上が偽の場合)、結果は偽

論理和(OR)

論理和(OR)とは

論理和(OR)は次のような演算です。

条件や主張A, Bのどちらかが真である時に結果が真、そうでない場合には結果が偽になる二項演算
- 論理和の演算式を、本記事ではA OR Bと表す
「ふたつの条件のどちらかが成り立つ(必要がある)場合」「ふたつの条件のうちどちらかが必要である場合」などを表すのに用いる（「どちらかが成り立てばよい」と理解しても差し支えないことも多い）
日本語では「または」「あるいは」「ないし」などの接続語が相当する
- 「ないし」は数量の範囲を表す意味もあるので注意が必要です（第5回に記載予定）

論理和の真理値表を図3-6に示します。

表の1～3行目が「A, Bのどちらかが真である時」
- “A, Bがともに真”である場合を含む
4行目が「そうでない(A, Bのどちらかが真、ではない)場合」

演算対象が三つ以上の場合

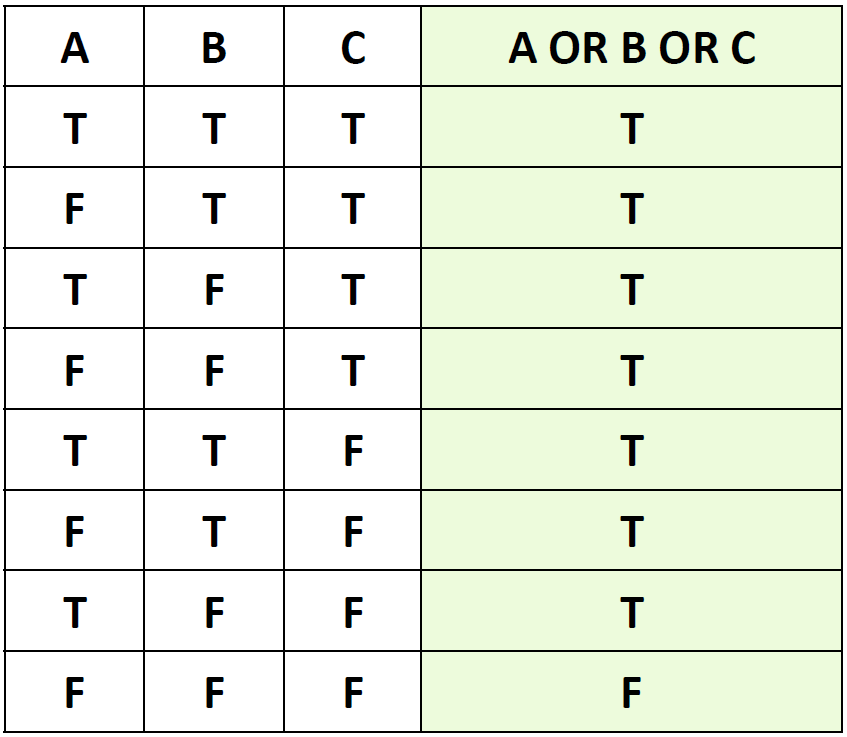
論理和は二項演算ですが、演算対象が三個以上になっても同じように考えることができます。（三条件の論理和の真理値表は図3-7参照）

演算対象がどれがひとつ以上が真の時、結果が真
そうでない場合(＝すべてが偽の場合)、結果は偽

論理演算で表す例

第1回で出てきた「登録できるユーザーアカウント名」の例を見てみましょう。

登録できるユーザーアカウント名には以下の条件があります。
(a) アカウント名に使える文字は以下のいずれかに限ること
  半角英大文字(A～Z), 半角英小文字(a～z), 半角数字(0～9)
(b) アカウント名は16文字以下であること
(c) 既に登録済みのアカウント名は登録できない

a, b, cの条件をすべて満たしているときに登録できる(3条件の論理積)、と解釈すると（条件aはいったん「使用可能な文字だけで構成されている」と置き換えます）、

使用可能な文字だけで構成されている AND
16文字以下である AND
NOT(既に登録済み)

といった形に表せます。

条件a「使用可能な文字だけで構成されている」を展開すると

半角英大文字である OR 半角英小文字である OR 半角数字である

となります。

条件bを「16文字を越えていないこと」と読んで、否定を使って

NOT(16文字を超えている)

と表すこともできます。

むすび

例が既にそうなっていますが、これらの論理演算は組合せて使うことが多いです。

第4回では、この「論理演算の組み合わせ」の扱い方や、憶えておきたいことを見ていきます。

参考文献

『プログラミング言語C　第2版』(カーニハン, リッチー / 共立出版)
『プログラミング言語AWK』(エイホ, ワインバーガー, カーニハン / USP研究所)
JavaScript リファレンス (Webページ)
- https://developer.mozilla.org/ja/docs/Web/JavaScript/Reference
- 否定は「単項演算子」のカテゴリーで「論理否定」として、論理積と論理和は「バイナリー論理演算子」というカテゴリーで取り上げられている。（この「バイナリー」は二項演算の意か）
Python 言語リファレンス (Webページ)
- https://docs.python.org/ja/3/reference/index.html
- 「6.11. ブール演算 (boolean operation)」で取り上げられている。
『スマリヤン先生のブール代数入門』(スマリヤン / 共立出版)
『記号論理学　一般化と記号化』(スマリヤン / 丸善出版)
『入門！論理学』(野矢茂樹 / 中央公論新社)