テストエンジニアが身につけておきたいスキルの一つ「論理のスキル」。
「論理の言葉」の意味や働きに注意が向くようになったら、文や文章の読み書きで実践していきましょう。
この連載では、「論理スキル“実践編”」と題して、「文章の筋道を把握する、主張を理解する」「文や文章の筋道を組み立てる」ことに役立つ推論の形を見ていきます。
＜テストエンジニアのための論理スキル[実践編] 連載一覧＞※クリックで開きます
・ 論理のかたち。推論とは 【連載初回、全文公開中】
今回のテーマは「基本的な推論形式」です。
「推論」と言われると難しそうに感じるかも知れませんが、“入門編”で見た「論理の言葉」が基本になります。
「論理の言葉」を復習してから、推論を支えてくれる基本的な形を見ていきましょう。
前回のクイズ解答
前回、「論理のかたち。推論とは」で出題したクイズの解答です。
（問1, 2とも、今回の内容でおさらいしています）
問1
Aさんの性格を考えると、①Aさんはギャンブルに手を出すと破産する。
しかし、②Aさんはギャンブルには手を出さない。
従って、③Aさんは破産しない。
①は「PならばQ」という条件法の形をしています。 ②③は①に対し「PでないならばQではない」という、“裏”の形をしていますが、これはよい形ではありません。
問2
その時代、①家柄がよくて、裕福ならば、誰でも結婚できた。
②彼の家柄はよかった。
しかし、③結婚できなかった。
従って、④彼は裕福ではなかった。
①は「(PかつQ)ならば、R」という形をしています。③の「Rではない」から、「Rでないならば、(PかつQ)ではない」という対偶の形が考えられます。「(PかつQ)ではない」ということは、「Pでないか、またはQでない」ということです（ド・モルガンの法則）。
②でPであることが言われているので、「Pでない」可能性は消え、残る「Qでない」が結論として④で述べられています。この主張はよい形をしています。
推論を形づくる“道具”
推論で大切なのは、前提から結論まで筋道を立ててつなげていくことでした。その筋道は、「論理の言葉」をいわば“道具”として作ります。
この“道具”の使い方をよく理解しましょう。
文と文を繋げる道具 ――論理の言葉おさらい
基本の論理演算：AND/OR/NOT
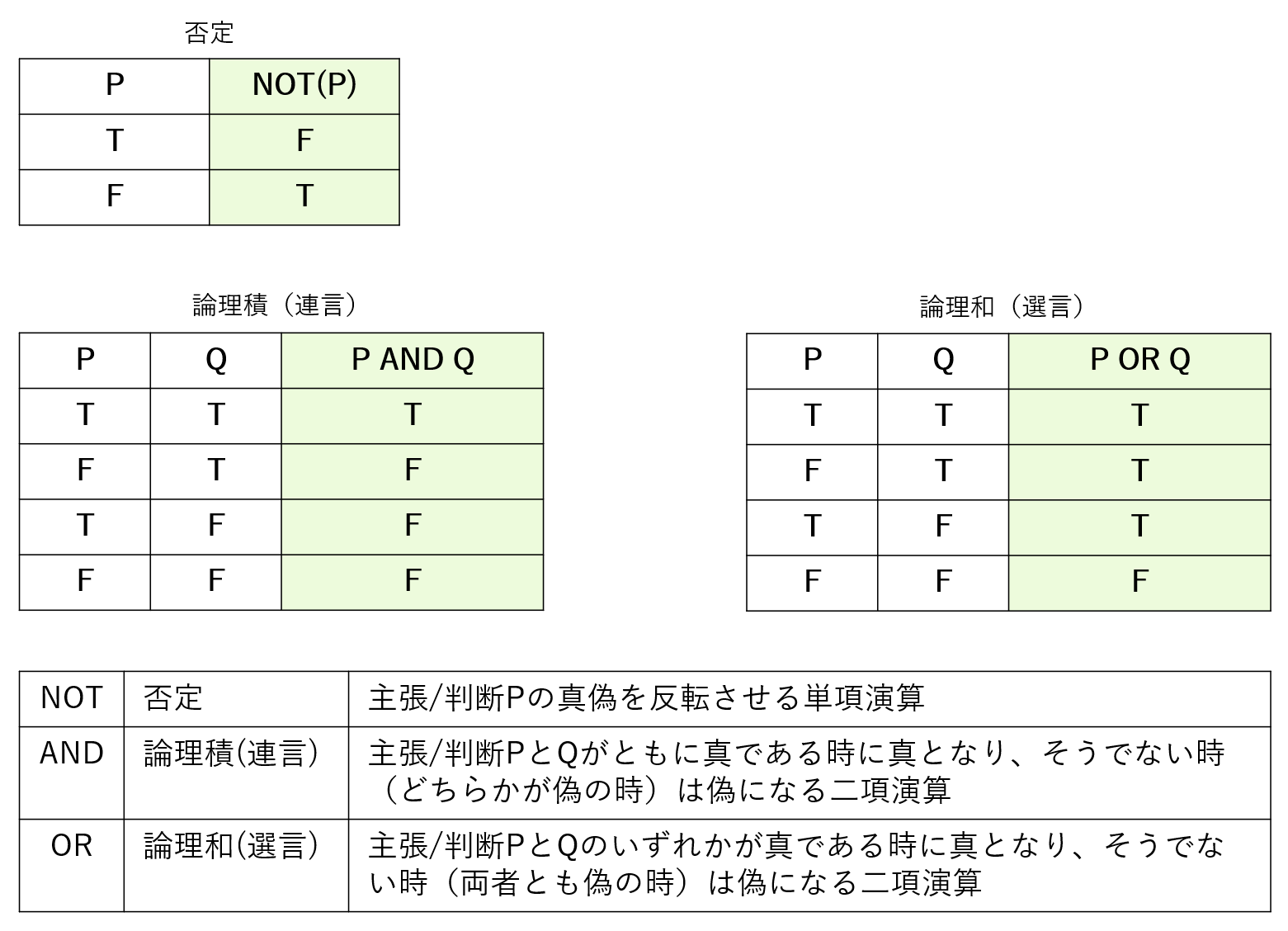
論理の言葉の基本のうち、論理演算、AND(論理積)、OR(論理和)、NOT(論理否定)の真理値表を図2-1に示します。（“入門編”第3回 基本の論理演算）
“ならば”と、等値(同値)の“ならば”
条件・場合を表す言葉“ならば”(条件法)と、等値の“ならば”(双条件法)も、論理の言葉の基本でした。（“入門編”第6回 条件・場合を表す言葉）
これらにも真偽があり、真理値表で表すことができます。 「“ならば”という言葉の働きが成り立つ場合(真)と成り立たない場合(偽)がある」と考えてください(図2-2)。
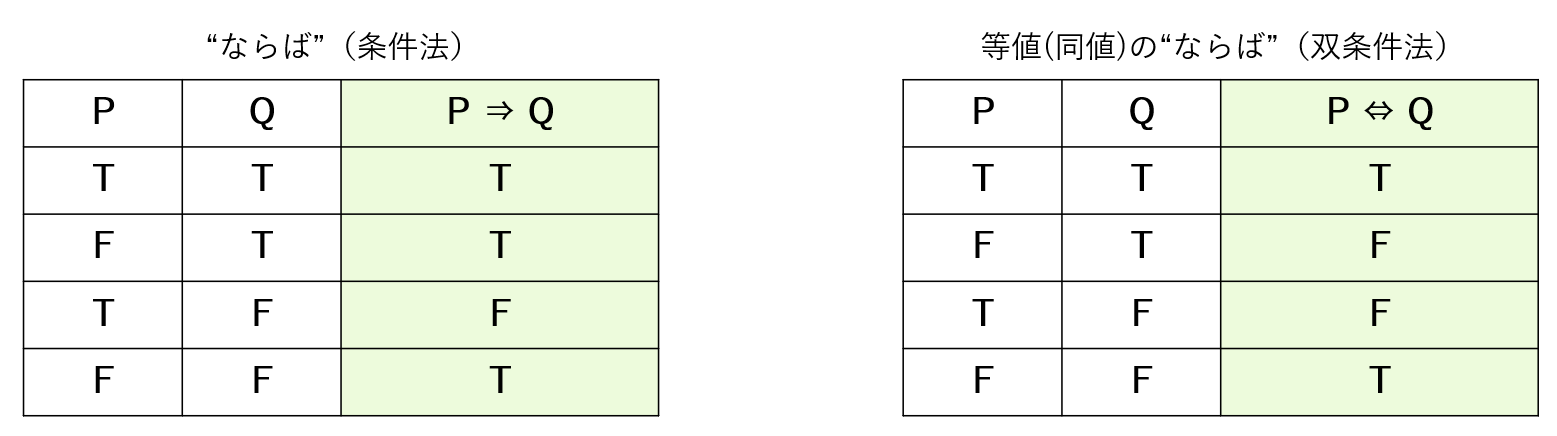
条件法の真理値表(図2-2 左)で「おや？」と思うところがありませんか？
2行目・4行目。Pが偽の時、Qが真でも偽でも“ならば”は真となっています。
これは条件法の「Pが真でない時」のことは何も言っていないという性質に由来します。何も言っていないのだから、Qが真でも偽でも“ならば”自体は成り立つ、「あり」とする、という約束、取り決めと考えてください。（なお、この性質を悪用すると、とんでもないことも「妥当な推論」として言えてしまいます）
3行目。「PならばQ」は、「Pが真なのにQが偽であることはない」という意味です。そこで、Pが真でQが偽の場合は、条件法は偽(成り立たない) と考えます。
“実践編”での呼び方：選言、連言、仮言、定言
論理積/論理和といった用語に代えて、“実践編”では、堅い響きですが短い呼び方を用います。
- 論理積(“かつ”)を連言とも呼びます。ふたつの主張/判断が連なっているイメージですね。
- 論理和(“または”)を選言とも呼びます。ふたつの主張/判断のいずれかを選び取るイメージですね。
- 条件法(“ならば”)は仮言とも呼びます。“ならば”を用いた主張/判断を仮言文(仮言判断)と呼びます。
- 仮言文に対し、「ネコは哺乳類である」「ネコは鳥類ではない」といった断言形式の主張を、定言文(定言判断)とか断言文(断言判断)と呼びます。
基本的な推論形式 (1) “入門編”で見たことのあるもの
論理の言葉はそのまま使える
前章でおさらいした基本的な論理の言葉の性質や働きと、次に挙げる論理の言葉の働きは、そのまま推論に用いることができます。
図2-3で、⇔の左辺の形は右辺の形に、右辺の形は左辺の形に言い換えることができます (前回のクイズ参照)。
- 二重否定は“入門編”第3回 基本の論理演算参照
- ド・モルガンの法則は“入門編”第4回 論理演算の組合せ参照
3・条件法と対偶に関して、逆（QならばP）と裏（PでないならばQでない）は一般には正しくないことも思い出しましょう。
4・条件法の言い換えについて。Pの否定・NOT(P)とQとのORをとると（NOT(P) OR Q）、“ならば”と同じ真理値の表が得られます(図2-4)。
この関係から、「PならばQ」は「Pでないか、またはQである」と言い換えて考えることもあります（このように同じ真理値を持つ論理演算どうしの関係も“同値”と呼びます）。
基本的な推論形式 (2) ちょっと複雑な形
推論を形づくる論理の言葉
論理の言葉を組み合わせて、複雑な推論の形を組み立てることができます。その中でも基本的な形とされているものをいくつか図2-5に示します。
6は“または”の意味/働きを使った推論で、選言三段論法と呼ばれます。
7, 8, 9は、“ならば”の意味/働きからこのような推論ができます。 7は前件肯定、8は後件否定というもので、9は“ならば”を重ねています。 併せて仮言三段論法と呼ばれます。
10, 11は複雑さが増して感じられますが、「AかBかどちらか」ということを言い表すのに使います。これらは両刀論法(ディレンマ, ジレンマ)と呼ばれる形です。
次回以降、これらの推論形式を詳しく見ていく予定です。
「当たり前」には裏づけがある
図2-5、（10, 11は別としても）どれも「当たり前では？」と思う人も多いでしょう。実際、これらは私たちの日ごろの思考に通じているものがあります（というか、「私たちの思考」を吟味して論理の言葉や推論の形式ができているのですが）。
この「当たり前」は論理の言葉が保証してくれている、裏づけがある、と知っておくのは大切なことです。 「よい形」であるのは、当たり前だからなのではなくて、「論理の言葉の使い方として正しいからよい形（妥当）」ということです。
三段論法
2,000年以上の歴史を持つ推論の形
前章で三段論法という言葉が出てきました。
前提2個に結論1個で構成されるから「三段論法(syllogism)」と呼ばれます（前提の数は3個以上でもよい）。 「大前提、小前提、結論」という用語の組を聞いたことのある人も多いでしょう。
ふたつの前提に論理の言葉の働きを作用させたり、主張している事柄の関係性を考慮したりして、結論を引き出すようになっています。
“定番”の三段論法
「三段論法」と言われたら、多くの人は次の形のものを思い浮かべるのではないでしょうか（“または”も、“ならば”も、使われていません）。
人間は誰しも死ぬ。
ソクラテスは人間である。
ゆえに、ソクラテスは死ぬ。
これを見て「当たり前のことを言っているなあ」と思う人も多いと思いますが（筆者もそうです）、この形はこの形で私たちのものの考え方に根ざしており、知っておく意義はあります。
この形の三段論法は連載後半で取り上げる予定です。
クイズ
（解答は次回に）
次回予告
先の「基本的な推論形式 (2)」で出てきた「“または”を使う推論の形（選言三段論法）」を詳しく見ていきます。
参考文献
- 近藤洋逸, 好並英司 『論理学入門』 岩波書店 1979
- John Nolt, Dennis Rohatyn(著), 加地大介(訳) 『現代論理学 (Ⅰ)』 オーム社 1995
- 鈴木美佐子 『論理的思考の技法Ⅱ』 法学書院 2008
- レイモンド・スマリヤン(著), 高橋昌一郎(監訳), 川辺治之(訳) 『記号論理学 一般化と記号化』 丸善出版 2013
図版に使用した画像の出典
- TopeconHeroesダーヤマ, 『分かりやすいプレゼン資料 1秒で伝わるビジネスイラスト集』 インプレス 2016
- クイズの画像に使用しています。
