[第4回] プログラムレベルのロジック (3)解説編・論理演算の組合せ

テストエンジニアが身につけておきたいスキルの一つに「論理スキル」があります。

この連載では、「プログラムのレベル」「文や文章のレベル」に分けて、論理スキルの基本である「論理の言葉」を徹底解説します。

筆者のnoteサイトで、「論理スキル[再]入門」を書こうと思った理由・経緯を綴っています。
■論理スキル・“入門編”のこと　(T3:Pt1:Ch01)
よろしかったらご覧ください。

今回第4回は、第3回で見た論理演算の組合せについて解説します。

＜テストエンジニアのための論理スキル[再]入門　連載一覧＞※クリックで開きます

論理演算の組合せ①

第3回で出てきた3条件の論理積や論理和や、「登録できるアカウント名文字列の条件」（3条件の論理積として扱いました）は、実は「二項演算である論理積/論理和の組合せ」です。（図4-1参照）

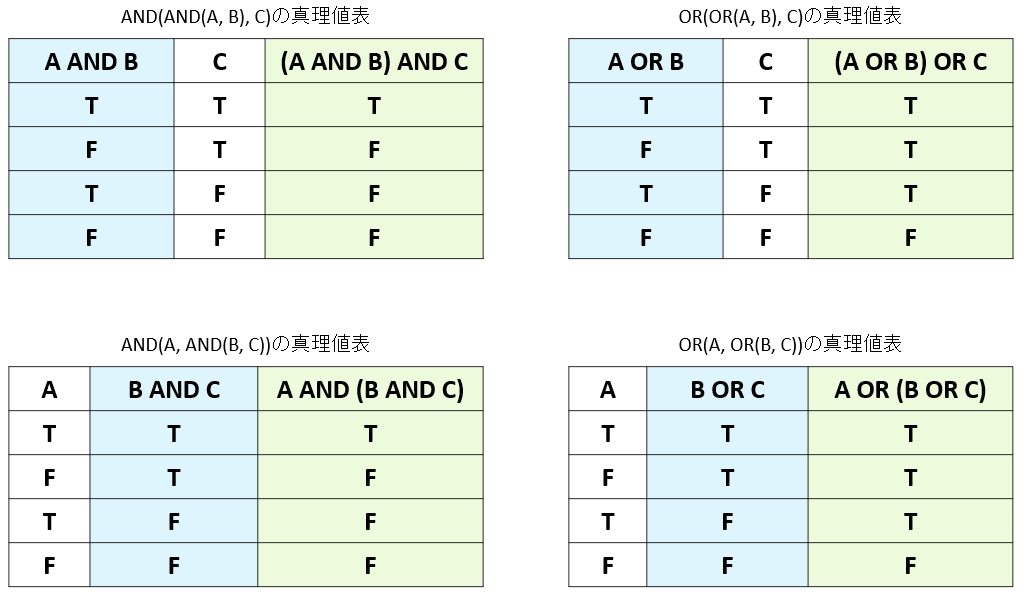
もっと“複雑”な組合せができることもあります。たとえば次のような、ふたつの数値がそれぞれ所定の範囲にあるという条件は……

入力Aの数値がminA以上で、かつ、入力Aの数値がmaxA以下である　か、
または、
入力Bの数値がminB超で、かつ、入力Bの数値がmaxB未満である

次の三つの論理演算の組合せでできていますから……

論理演算の式として下記のように表せます：

(A >= minA AND A <= maxA)
OR
(B > minB AND B < maxB)

論理演算を組み合わせる時は、何と何がAND/ORの関係にあるかに気をつけましょう。

個々の論理演算式を丸括弧”()”で括ると、書き間違い・読み間違いを抑えられます。

（「登録できるアカウント名」を、使用可能な文字(3条件のOR)をまとめずに論理演算の式で表してみてください）

組合せの中で、AND式やOR式をNOTで括った「AND式の否定」「OR式の否定」はよく出てきます。テストを考える時にも頻繁に出くわす形です。

という仕様があった場合、テストとしてはS1, S2それぞれについて次の両方を考えます。

S1のEiはAND式の否定・NOT(A AND B)、S2のEiはOR式の否定・NOT(A OR B)です（図4-2, 4-3, 4-4）。

「条件を満たさない」場合のAとBの真偽はどう考えればよいでしょうか。

AND式/OR式とその否定(NOT)との関係を理解しやすくしてくれるのがド・モルガンの法則です。

A AND B(Aであり、かつ、Bである)の否定　⇔
Aの否定か、または、Bの否定（Aでないか、または、Bでない）
- NOT(A AND B) ⇔ NOT(A) OR NOT(B)
A OR B(Aであるか、または、Bである)の否定　⇔
Aの否定、かつ、Bの否定（Aでなく、かつ、Bでない）
- NOT(A OR B) ⇔ NOT(A) AND NOT(B)
この関係は常に成り立つ。（図4-5, 4-6）

「買い上げ点数が5点以上」を条件A, 「買い上げ合計額が2,000円超」を条件Bとすると、

「買い上げ点数が20点以上」を条件C, 「買い上げ合計額が10,000円超」を条件Dとすると、

ド・モルガンの法則は、今回冒頭に挙げた「2変数の数値の範囲の組合せ」のような、込み入った論理演算の組合せにも当てはまります。

考えやすくするために、A, Bの範囲を表す詳細な条件式を“まとめて”表します。

NOT(𝔸)について
- 展開すると　　　　　　　　…… ＝　NOT(A >= minA AND A <= maxA)
- ド・モルガンの法則を適用して　 ⇒　NOT(A >= minA) OR NOT(A <= maxA)
- 否定を取り除いて(不等号を逆転)　⇒　A < minA OR A > maxA
NOT(𝔹)について
- 展開すると　　　　　　　　…… ＝　NOT(B > minB AND B < maxB)
- ド・モルガンの法則を適用して　 ⇒　NOT(B > minB) OR NOT (B < maxB)
- 否定を取り除いて(不等号を逆転)　⇒ 　B <= minB OR B >= maxB
⇒(A < minA OR A > maxA) AND (B <= minB OR B >= maxB)
＝「『入力AがminA未満であるか、または、maxA超』であり、かつ、
『入力BがminB以下であるか、または、maxB以上』」