テストエンジニアが身につけておきたいスキルの一つ「論理のスキル」。
「論理の言葉」の意味や働きに注意が向くようになったら、文や文章の読み書きで実践していきましょう。
この連載では、「論理スキル“実践編”」と題して、「文章の筋道を把握する、主張を理解する」「文や文章の筋道を組み立てる」ことに役立つ推論の形を見ていきます。
＜テストエンジニアのための論理スキル[実践編] 記事一覧＞※クリックで開きます
今回と次回で、「三段論法」と言われると思い浮かべる人が一番多いと思われる形式の三段論法を取り上げます。
今回はこの形式の三段論法の基本的な事項の紹介です。「大前提・小前提・結論」だけでなく、押さえておきたい事柄があります。なんとなく知っていたという人も、今回で「三段論法」の理解を深めましょう。
その前に、前回クイズの解答ですね。
前回クイズ解答
問題(再掲)
問1～問3の主張が両刀論法のどの形に該当するか、また妥当な形かどうか考えてください。
解答
問1。①のふたつの仮言判断A, Bは、前件も後件も異なります。②でA, Bそれぞれの後件を否定し、③でA, Bそれぞれの前件の否定を結論としています。複雑破壊的 両刀論法です。
問2。①のふたつの仮言判断A, Bは後件が同じです（プロジェクトが遅延する）。②でのA, Bそれぞれの前件肯定から、③A, Bの後件を結論としています。 単純構成的 両刀論法です。
問3。①の「新しいことを考える時間も減る」には、「テストに時間を割く」という前件が省略されている、つまり、前件が同じ仮言判断A, Bがあると考えられます。
②でA, Bそれぞれの後件を否定し、③でA, Bの共通の前件を否定しています。 単純破壊的 両刀論法です。
問1～問3のいずれも、形は妥当です。（内容については……どう考えますか？）
ソクラテスは電気羊の夢を見るか？
ソクラテスに申し訳ないので
いつも死なせてばかりでは申し訳ないので、ちょっと毛色を変えてみました。
図6-1の主張その1～3のそれぞれで、前提(①、②)から結論(③)が言えると思いますか？（内容の真偽ではなく、主張の形として）
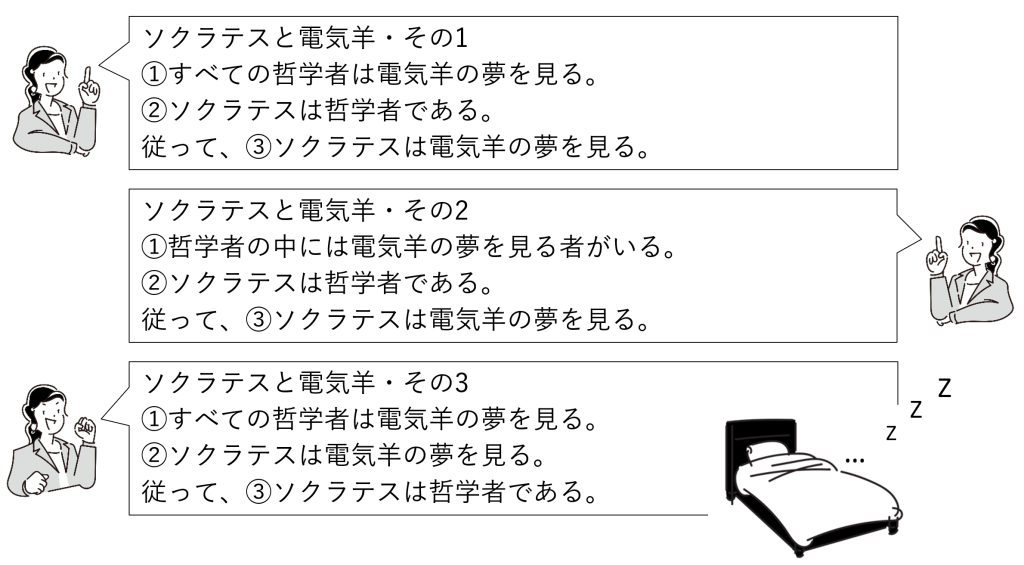
概念と概念の関係を推論する
「ソクラテスと電気羊」の特徴
「“ならば”と“または”で推論する」
の各回で見てきた三段論法は、文と文をつなぐ 論理の言葉 の意味と働きで結論を導き出していました。
「ソクラテスと電気羊」にはそのような論理の言葉は使われておらず、断定的な文が並んでいるだけです。
定言三段論法
このような、すべての文が断言形式の文で構成される形の三段論法を、定言三段論法 や断言三段論法といいます。
各文は 主語 と 述語 というふたつの言葉(概念)からなります。図6-1の例では、「ソクラテス」「哲学者」「電気羊の夢を見る」が主語や述語に当たります。
定言三段論法はこれらの文に現れる「言葉(概念)どうしの関係性」を論じるもので、前提に出てくる 主語と述語の関係（包含関係の成否） から結論を導き出します。
定言三段論法の構造
三つの概念：S, P, M
主語や述語は何かしらの概念を表す言葉で、S, P, Mの三種類が登場します。
- 小名辞(S)(小概念)：結論の主語 になる言葉(概念)です。
小名辞Sが現れる前提を小前提 と呼びます。 - 大名辞(P)(大概念)：結論の述語 になる言葉(概念)です。
大名辞Pが現れる前提を大前提 と呼びます。 - 媒介項(M)(中名辞、媒概念)：大前提、小前提の両方に現れ、SとPの間を取り持つ言葉(概念)です。
図6-1の例・その1では、「ソクラテス」が小名辞S、「電気羊の夢を見る」が大名辞P、「哲学者」が媒介項Mとなります(図6-2)。
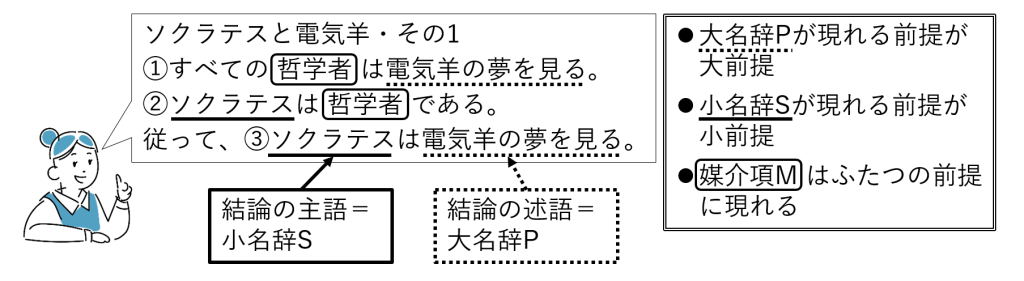
結論は常に「小名辞Sが主語、大名辞Pが述語」ですが、大前提、小前提では、S, P, Mが主語・述語のどちらになるかは主張内容によって変わります。
なお、小名辞・大名辞の区別は、それらが指す概念の大きさと一致するとは限りません。
文の並び：大前提→小前提→結論 とは限らない
慣習的には大前提・小前提・結論と並びますが、これは決まりではなく、三つの文はさまざまな並びがあり得ます（3つの文を並べる順列ですから、6通り）。「結論を最初に述べて、その理由や根拠として大前提・小前提を述べる」といった並びはよく見かけます。
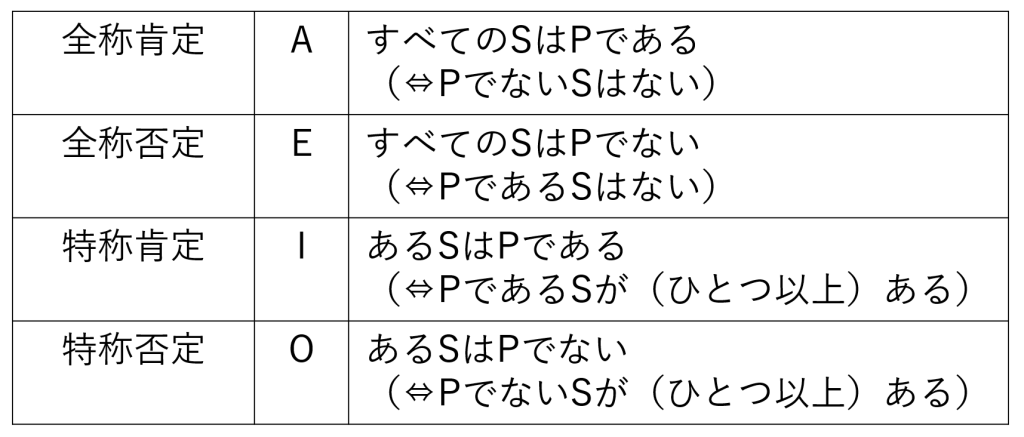
文の種類：AEIO
大前提、小前提、結論の各文には、主語と述語に関して 修飾 がかかります(図6-3)。
- 主語の概念が適用される範囲（判断の「量」といいます）。
その範囲によって 全称 と 特称 に分かれます。- 全称判断：主語の概念が当てはまる全体について述べる文。例：「すべての SはPである」
- 特称判断：主語の概念が当てはまるうちの一部について述べる文。例：「ある SはPである」
- ※固有名詞は全称として扱います。
- 述語にかかる判断の性質（判断の「質」といいます）。
肯定 と 否定 があります。- 肯定判断：述語が当てはまると主張する文。例：「すべてのSはP である」
- 否定判断：述語が当てはまらないと主張する文。例：「すべてのSはP でない」
全称/特称と肯定/否定の組合せで、A, E, I, O, 4つの種類の文があります(図6-4)。表中の丸括弧内は、同じことを言い換えた形です。
全称否定(E)に注意してください。文全体を否定する（「すべてのSがPである、というわけではない」）のではなく、述語だけを否定した「Sであるものはすべて、Pではない」という意味になります。
AEIOそれぞれにおける、主語と述語の包含関係は図6-5のようになります（Sが主語、Pが述語）。🙄(あるかも)は、その文では言及していない部分です（該当する要素があるかも知れない）。
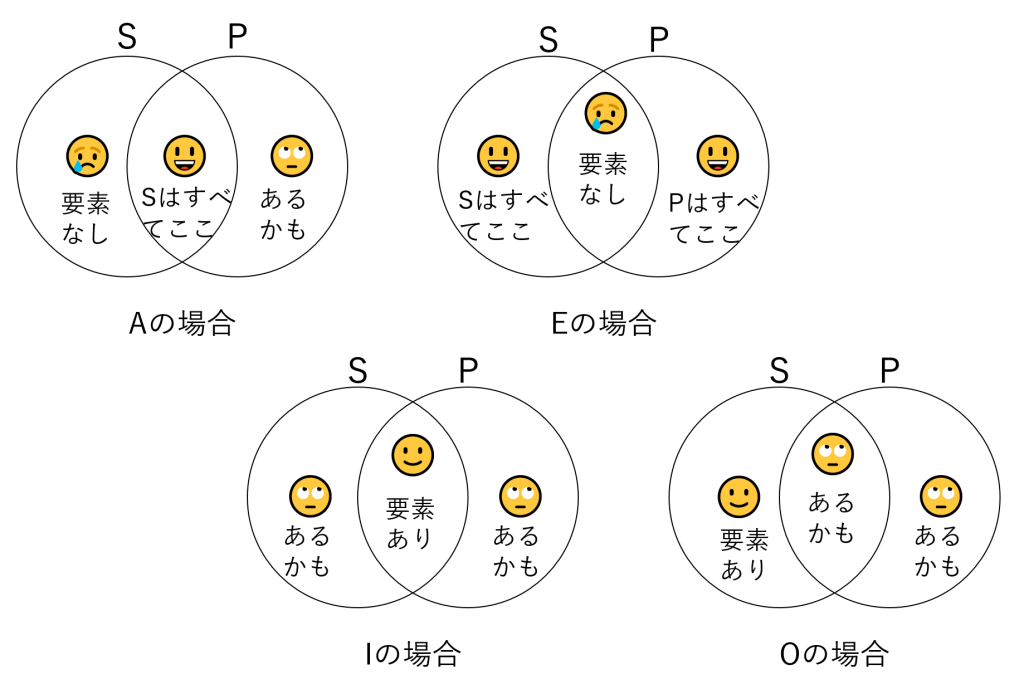
主語と述語の状態：周延
続きを読むにはログインが必要です。
ご利用は無料ですので、ぜひご登録ください。
