テストエンジニアが身につけておきたいスキルの一つ「論理のスキル」。
「論理の言葉」の意味や働きに注意が向くようになったら、文や文章の読み書きで実践していきましょう。
この連載では、「論理スキル“実践編”」と題して、「文章の筋道を把握する、主張を理解する」「文や文章の筋道を組み立てる」ことに役立つ 推論の形 を見ていきます。
＜テストエンジニアのための論理スキル[実践編] 記事一覧＞※クリックで開きます
今回は、条件を表す言葉“ならば”と、選言“または”を組み合わせた推論の形を見ていきます。
その前に、前回のクイズの答えです。
前回クイズ解答
問題(再掲)
問1～問3の主張は妥当でしょうか。推論の形に着目して考えてください。
解答
問1。混合仮言三段論法で、①に対する前件否定（②）から、①の後件の否定を結論としています（③）。形式上の誤りで非妥当です。
（実際、テストの期間・工数の超過を招く要因は、設計成果物の欠陥の多さ だけではありません）
問2。純粋仮言三段論法です（①～③までが前提）。仮言判断の連鎖から、①の前件と③の後件をつないだ仮言判断を結論としています。これは妥当な形です。
問3。純粋仮言三段論法＋混合仮言三段論法といった形です（③が②を承けた断言判断）。③が②に対する後件肯定であり、④で①の前件の肯定を結論としています。形式上の誤りで非妥当です。
（テスト結果がおかしくなる原因はテストデータの誤り 以外にもあり得ます）
ふたつの“ならば”と、“または”で推論する
両刀論法(ディレンマ, ジレンマ)とは
図5-1のような形の推論を 両刀論法 といいます。
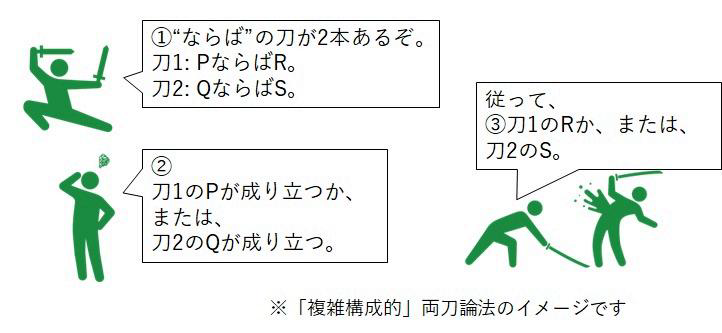
ふたつの仮言判断（条件法を使った文）に対して選言判断を組み合わせて結論を導きます。
両刀論法の形式の例(複雑構成的)
図5-1で示した形は、「複雑構成的」両刀論法 といいます。
①PならばR、かつ、QならばS。
②Pか、またはQ。
従って、③Rか、またはS。
- 前提1で、ふたつの仮言判断A, Bを並べ、
「どちらも、前件が成り立つなら後件は成り立つ」という主張をします。 - 前提2で、ふたつの仮言判断の 前件のどちらかは真だ と主張します
（Aの前件が真であるか、または、Bの前件が真）。 - すると、前件肯定 から結論「ふたつの仮言判断の 後件のどちらかは真だ」が浮かび上がってきます(図5-2)。
（前件肯定は、「“ならば”を使って推論する」参照）
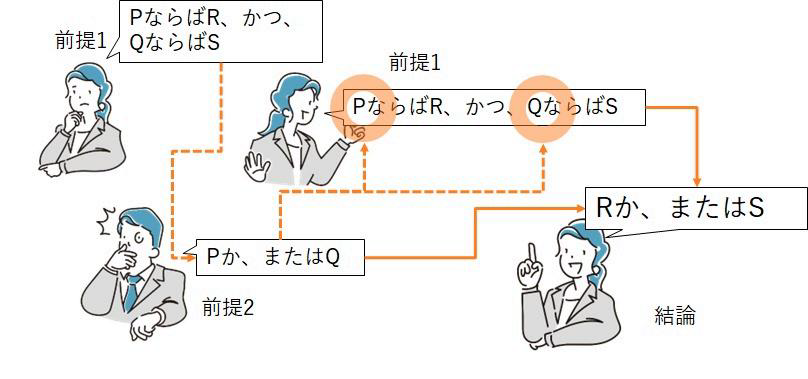
前提1は、条件つきの主張をふたつ提示するのが主眼です。本記事では形を示すのに連言（“かつ”）で表していますが、連言の形を取らない例も多く見られます。
例。
①明日が雨なら、Aさんは自宅にいるでしょう。明日雨が降らないなら、Aさんはサイクリングを楽しむでしょう。
②明日は雨が降るか、降らないか、どちらかです。
従って、③明日Aさんは自宅にいるか、サイクリングをしているか、どちらかです。
ディレンマ, ジレンマ
両刀論法は英語では「ディレンマ, ジレンマ(dilemma)」と呼ばれます。
「ジレンマ」は、古代ギリシャ語の「ディレンマ」（dilemma）が語源である。
ディレンマは、「二つの前提」を意味する「ディ」（di）と、「仮定」を意味する「レンマ」（lemma）が組み合わさった言葉である。
weblio辞書「ジレンマ」から
日本語では、“ジレンマ”は「ふたつの選択肢のどちらを選んでも困ったことになる“板挟み”の状態」といった意味で使われることが多いと思われます。
先の複雑構成的の形で、Qを「Pでない(NOT(P))」と置くと、
- ①PならばR、かつ、NOT(P)ならばS。
- ②Pか、または、NOT(P)。
- 従って、③Rか、またはS。
PとNOT(P)のどちらかにならざるを得ず、RもSも好ましくない結果なら、典型的なジレンマが出現します。
例。(笑えません)
①テストを続けるならば、テスト期間が伸びてリリースが遅れることになる。テストを止めるならば、テスト不足のままリリースすることになる。
②テストを続けるか、止めるかのどちらかだ。
従って、③リリースが遅れるか、テスト不足の製品をリリースするかのいずれかだ。
しばしば聞く言葉ですし、案外よく見かける立論の形式ですから、こういう推論の形があることとその特徴を知っておくのは有益でしょう。
両刀論法
両刀論法の形：単純/複雑と、構成/破壊
両刀論法は、
- 前提1は、ふたつの仮言判断
- 前提2は、前提1の各仮言判断の 肯定(前件の肯定)、または 否定(後件の否定)
という形を取ります。
前提1に着目して、単純式/複雑式 と区分されます。
- 単純式：前提1のふたつの仮言判断の、 前件または後件が同じ
- 複雑式：前提1のふたつの仮言判断の、 前件/後件ともに異なる
前提2に着目して、構成式/破壊式 と分けられます。
- 構成式：前提2で、前提1のふたつの仮言判断の 前件を肯定 する
- 破壊式：前提2で、前提1のふたつの仮言判断の 後件を否定 する
- いずれも、前提2は選言
両刀論法の4つの形
前提1の単純/複雑、前提2の肯定/否定の組合せから、4通りの形があります(図5-3)。
説明済みの複雑構成的(図5-2)を基にすると考えやすいでしょう。
（「基本的な推論形式」では、複雑構成的と複雑破壊的のふたつを紹介しています）
複雑破壊的
複雑破壊的(図5-4)は、複雑構成的(図5-2)の前提2を、前件肯定（Pか、またはQ）から 後件否定（Rでないか、またはSでない） に変えた形です。
それぞれの後件が否定され、結論は前件の否定「Pでないか、またはQでない」 になります。
例。
①Bさんが参考書を読んでいるなら、この問題の解き方を知っている筈だし、この分野に詳しいなら、この問題の難しさを判っている筈だ。
②Bさんはこの問題の解き方を知らないか、この問題の難しさを判っていないか、どちらかだ。
だから、③Bさんは参考書を読んでいないか、この分野に詳しくない。
単純構成的
単純構成的(図5-5)は、複雑構成的(図5-2)の前提1におけるふたつの仮言判断の後件(R, S)をひとつ(Rのみ)にした形です。
前提2の前件肯定から、結論は後件の肯定 「Rである」になります。
例。
①スポーツを続けるなら、Cさんにとってはいい経験だし、スポーツを止めて別のことに取り組むなら、それもいい経験になる。
②Cさんはスポーツを続けるか、スポーツを止めるか、どちらかだ。
③いずれにしろCさんにはいい経験になる。
単純破壊的
単純破壊的(図5-6)は、複雑破壊的(図5-4)の前件(P, Q)をひとつ(Pのみ)にした形です。
単純構成的(図5-5)の、前提1の前件をPひとつに、後件を異なるふたつ(R, S)にし、前提2を前件肯定から後件否定に変えた形とも読めます。
前提2の後件否定から、結論は前件の否定 「Pではない」になります。
例。
①Dさんは、学校の試験の成績がよいと、帰宅してからとても明るいし、晩ご飯をよく食べる。
先週期末試験があったが、
②今週のDさんは毎日暗いか、ご飯をあまり食べないかのどちらかだ。
ということは、③Dさんは先の期末試験の成績がよくなかったのだな。
両刀論法・補足
排他的な“または”でも成り立つ
前提2と結論の選言(“または”)は、排他的な“または”でも成り立ちます。
“刀”が二本より多い場合
前提1の仮言判断が二つより多くても同じ形の推論ができます。仮言判断の数ごとに名前がついています(図5-7)。
両刀論法・気をつけたい落とし穴(誤謬)
後件肯定の誤謬、前件否定の誤謬
“ならば”を用いた条件つき主張(仮言判断)を使う推論ですから、形式面では仮言三段論法と同じ落とし穴があります。
構成式で、「Rか、またはS」(複雑構成的の場合）という 後件肯定 から結論として「Pか、またはQ」を引き出すのは誤った推論です（後件肯定の誤謬）。
破壊式で、「Pでないか、またはQでない」(複雑破壊的の場合）という 前件否定 から結論として「Rでないか、またはSでない」を引き出すのも誤った推論です（前件否定の誤謬）。
（「“ならば”を使って推論する」参照）
選言肢不完全の誤謬
内容面で気をつけるべきことのひとつには、選言三段論法で紹介した「選言肢不完全の誤謬」があります（「“または”を使って推論する」）。
前提1の仮言判断が主張したいことを網羅できていなかったら、不備のある推論になってしまいます。
仮言判断の前件と後件の関係性
選言肢不完全の誤謬に通じますが、前提1が：
- ふたつの仮言判断の関係が希薄だったり、
- それぞれの前件と後件のつながりに必然性がなかったり
するものだと、飛躍や抜けのある推論になってしまいます。
？？？な例。
①開発中の製品ですが、売上がよかったらボーナスが出ます。開発が失敗したら、その経験を論文にして発表できます。
②開発は成功するか、失敗するか、どちらかですが……
③ボーナスが貰えるか、または、論文を発表できます。（＝いずれにせよ得るものがあります！）
留意点
両刀論法は 内容が偽であっても形式上は妥当な(よい形の)主張 を作りやすく、かつ「いずれにせよ××」的な主張を作りやすいので、古来より詭弁によく用いられてきたとされます（形は整っているために、反駁・反論が面倒）。
詭弁のつもりはなくとも間違いが混入している可能性がありますから、この形の推論に出会った時にはその内容面をよく吟味するのが望ましいと言えるでしょう。
ジレンマという言葉が聞こえたら、「それは両刀論法のどの形に該当するだろう？」と考えてみるのもいいトレーニングになります（隠れている前件や後件を補う必要がある場合もありますが、それも含めて）。
なお、内容面の誤謬とその反論については、回を改めて紹介する予定です。
クイズ
問1～問3の主張はそれぞれ両刀論法のどの形に該当するでしょうか。また妥当な形でしょうか。（解答は次回に）
次回
「ソクラテスは死ぬ」でおなじみの（ではないかも知れませんが）、「三段論法と言われたらコレ、の三段論法」を取り上げます。
参考文献
- 近藤洋逸, 好並英司 『論理学入門』 岩波書店 1979
- 藤野登 『論理学 伝統的形式論理学』 内田老鶴圃 1968
- John Nolt, Dennis Rohatyn(著), 加地大介(訳) 『現代論理学 (Ⅰ)』 オーム社 1995
- 鈴木美佐子 『論理的思考の技法Ⅱ』 法学書院 2008
図版に使用した画像の出典
- ヒューマンピクトグラム2.0
- ピクトグラムをお借りしています。
- Loose Drawing
- 人物画をお借りしています。
