テストエンジニアが身につけておきたいスキルの一つ「論理のスキル」。
「論理の言葉」の意味や働きに注意が向くようになったら、文や文章の読み書きで実践していきましょう。
この連載では、「論理スキル“実践編”」と題して、「文章の筋道を把握する、主張を理解する」「文や文章の筋道を組み立てる」ことに役立つ 推論の形 を見ていきます。
＜テストエンジニアのための論理スキル[実践編] 記事一覧＞※クリックで開きます
前回「“または”を使って推論する」では、“または”という言葉(連言)を使った推論の形を取り上げました。
今回は、条件を表す言葉“ならば”(条件法)を用いた推論の形を見ていきます。
前回クイズ解答
問題(再掲)
※第3回の問題で、図版に誤りがございました（問3が間違っています）。
ご覧になった方を混乱させたことをお詫び申し上げます。
以下に正しい図を掲載します。
解答
問1。「Pか、またはQ」に対して、一方の否定から他方の肯定を結論する、選言三段論法の妥当な形をしています。
問2。一方の肯定から他方の否定を結論とする、選言三段論法の妥当でない形です。実行手順の問題とテスト環境の問題は両立し得る事象です。
問3。ふたつのモードは「相互に切り替えて利用できる」ことから、同時には一方のみが有効と考えられます。排他的な“または”と言えるので、この推論は妥当です。
仮言三段論法 ― “ならば”を使って推論する
“ならば”の性質と推論
こんなことを言われても――
今日中にリリースがないなら、明日のテストは中止だ。
これだけでは明日のテストについてはなんとも判りません。
が、ここに「今日はリリースはないってよ」という情報が加わると、「明日のテストは中止だ」と断言してよさそうに思えてきます。
あるいは、「例の課題を解決できないなら、今日中のリリースはない」といった情報が加わると、「例の課題が解決できないなら、明日のテストは中止だ」という新たな主張が得られます。
“ならば”(条件法)は推論で大活躍をする論理の言葉で、考えを進めたり議論をしたりする際に、言葉を変えたり隠れたりして頻繁に現れます（この節にも2ヶ所隠れています）。
この言葉を使った推論のよい形・よくない形を理解しておきましょう。
“ならば”を使って、前提から結論を導く
前提1が仮言判断（“ならば”を用いた条件つきの主張）である推論を 仮言三段論法 といいます（文献によっては、条件三段論法とも）。
前提2にどんな文が来るかによって、純粋仮言三段論法 と 混合仮言三段論法 があります(図4-1)。
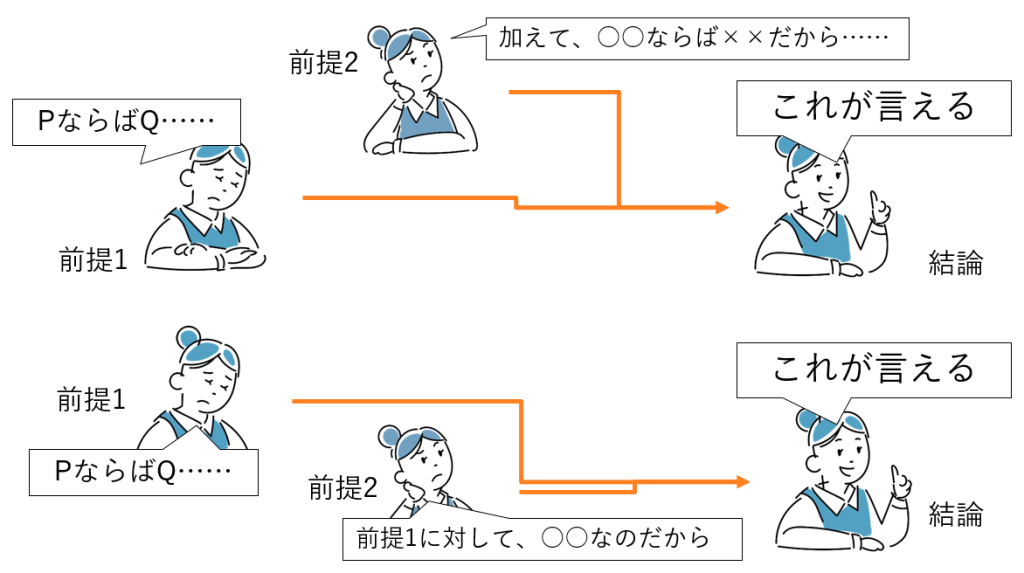
- 純粋 仮言三段論法(図4-1 上)：前提2も仮言判断。結論も仮言判断になる
- 混合 仮言三段論法(図4-1 下)：前提2が断言判断。結論は断言判断になる
混合仮言三段論法から説明します。
混合仮言三段論法
“ならば”と、断言を組み合わせる
前提1「PならばQ」に対する断言形式の主張を前提2で述べることで、結論を引き出します。結論は断言判断 になります。
ふたつの形があります。
混合仮言三段論法・(1)肯定式(前件肯定)
ひとつめは、前提1「PならばQ」に対して「P(前件)は成り立つよ」と言う形です(図4-2)。
①PならばQ。
②P。
従って、③Q。
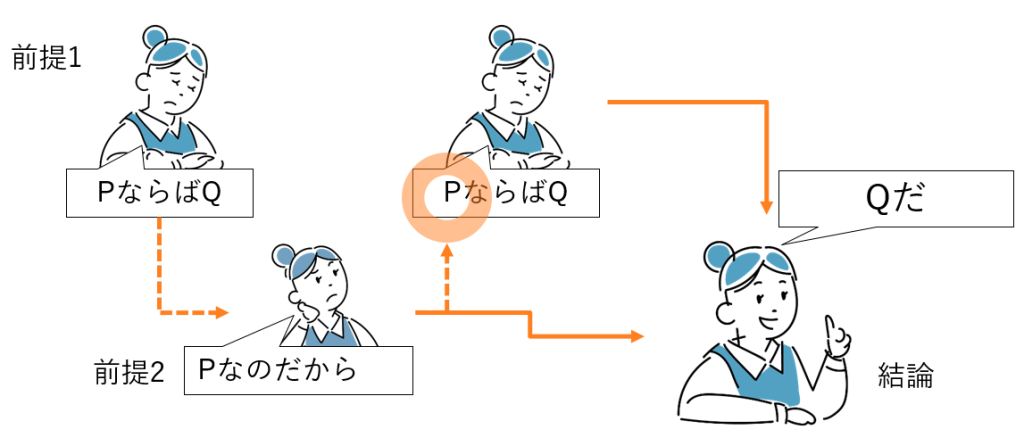
①「PならばQ」に対して、②「P(前件)が真」が加わると、③「Qは真」が結論として導けます。
この形は「肯定式(Modus Ponens, MP)」「前件肯定」 と呼ばれます（文献によっては構成式とも）。
「論理のかたち。推論とは」冒頭の例でいうと：
例：
①雨が降っているなら、Aさんは自宅で過ごす。
②今日は雨だ。
だから、③今日、Aさんは自宅にいる。
混合仮言三段論法・否定式(後件否定)
ふたつめは、「Q(後件)は成り立たないよ」と言う形です(図4-3)。
①PならばQ。
②Qではない。
従って、③Pではない。
①「PならばQ」の対偶は、「QでないならばPではない」です。そして②「Q(後件)が偽（＝Qではない）」から、③「Pは偽（＝Pではない）」という結論が得られます。
この形は「否定式(Modus Tollens, MT)」「後件否定」と呼ばれます（文献によっては破壊式とも）。
例：
①雨が降っているなら、Aさんは自宅で過ごす。
②今日、Aさんは自宅にいない。
だから、③今日は雨は降っていない。
推論の重要なツール
前件肯定、後件否定は、“ならば”(条件法)の意味/働きから出てくる、とても重要な推論の形です。
条件つきの主張から結論を引き出したり、考えや議論を進めたり、話の筋道を確かめたり見直したりするのに欠かせません。
対偶と併せてセットで憶えましょう。
純粋仮言三段論法
“ならば”を重ねる
前提1, 2とも“ならば”を用いた言明(仮言判断)で、ふたつの条件つき主張のつながりから結論を引き出します。
この形では、結論も仮言判断 になります。
“基本形”
「基本的な推論形式」で紹介したものが基本的な形です(図4-4)。
①PならばQ。
②QならばR。
従って、③PならばR。
（前提1, 2の順序は替わっても問題ありません）
「PならばQ」の後件Qが別の主張「QならばR」の前件となって両者をつなぎ、「PならばR」という主張を導いています。
例：
①雨が降っているなら、Aさんは自宅で過ごす。
②Aさんが自宅にいるなら、Aさんは趣味のギターに没頭する。
だから、③雨が降る日はAさんは自宅でギターを弾いている。
この基本的な形から、多くの推論の形が導出できます。
“ならば”をさらに重ねる
前提が3つ(以上)ある形は、込み入った主張の展開でよく見かけます。
①PならばQ。②QならばR。（……）③RならばS。従って、③PならばS。
一見飛躍があるように感じられる主張も、間をつなぐ条件つき主張が隠れていて、それを解き明かしていくとこの形の推論が浮かび上がることがあります。
対偶を織り込む
前提から結論の間に対偶が活躍することもあります。例をふたつ挙げます。（頭に「？」が浮かんだら、P, Q, Rの関係を図に書いてみてください）。
①PならばQ。②RならばQではない。従って、④PならばRではない。
①QならばR。②QでないならばP。従って、④PでないならばR。
前件肯定や後件否定との“合わせ技”
仮言判断の連鎖の後に前件肯定が来て：
①PならばQ。②QならばR。（……）③P。従って、④R。
また、後件否定が来て：
①PならばQ。②QならばR。（……）③Rではない。従って、④Pではない。
といった、長めの混合仮言三段論法といった感じの推論も作れます。
前提を否定する結論が出てきたら！？
時にはこんな形の推論も――
①PならばQ。②QならばR。（……）③RならばPではない。従って、④PならばPではない。
「Pが成り立つなら～」から始まって結論が「Pは成り立たない」となったら 矛盾 であり、話の筋道に問題がある証拠です。
意図せずしてこういう状態に陥ったら推論を見直すことになりますが（前提の真偽や、条件法の前件・後件の関係を確かめましょう）、
「前提が間違っている」ことを示すためにこういう推論を立てることもあります。数学の 背理法 が有名ですね。
仮言三段論法・気をつけたい落とし穴(誤謬)
後件肯定、前件否定
「前件肯定」「後件否定」とよく似た言葉で、「後件肯定」「前件否定」 があります。
これらは一般に 妥当でない形 です。違いに気をつけてください(図4-5, 4-6)。
- 後件肯定の誤謬(図4-5上)：①PならばQ。②Q。従って、③P。
- 前件否定の誤謬(図4-5下)：①PならばQ。②Pではない。従って、③Qではない。
「PならばQ」に対して、後件肯定は「QならばP」という“逆” を主張しています。前件否定は「PでないならばQではない」という“裏” を主張しています。元の主張が真でも、“逆”や“裏”は一般に真ではありません（QだからといってPであるとは限らないし、PでなくてもQである場合がある）(図4-6)。
前提の仮言判断（条件つき主張）の内容に注意
仮言三段論法は“ならば”の意味・働きに依存しています。
もっともらしい主張と感じられるならなおさら、主張内容の真偽を吟味することが大切です。
- 前件、後件の真偽
- 前件と後件の関係性（つながりに必然性はあるか、関連しているか）
クイズ
問1～問3の主張は妥当でしょうか。推論の形に着目して考えてください。（解答は次回に）
次回
「基本的な推論形式」で出てきた「両刀論法」を詳しく見ていきます。
参考文献
- 近藤洋逸, 好並英司 『論理学入門』 岩波書店 1979
- 藤野登 『論理学 伝統的形式論理学』 内田老鶴圃 1968
- John Nolt, Dennis Rohatyn(著), 加地大介(訳) 『現代論理学 (Ⅰ)』 オーム社 1995
図版に使用した画像の出典
- Loose Drawing
- 人物画をお借りしています。
