テストエンジニアが身につけておきたいスキルの一つ「論理のスキル」。
「論理の言葉」の意味や働きに注意が向くようになったら、文や文章の読み書きで実践していきましょう。
この連載では、「論理スキル“実践編”」と題して、「文章の筋道を把握する、主張を理解する」「文や文章の筋道を組み立てる」ことに役立つ 推論の形 を見ていきます。
＜テストエンジニアのための論理スキル[実践編] 記事一覧＞※クリックで開きます
前回の「ソクラテスは電気羊の夢を見るか？(前編)」では、「定言三段論法」と呼ばれる推論形式の基本事項を紹介しました。
定言三段論法的な推論を自分から意識して組み立てることは少ないかも知れませんが、考えを整理してみたら定言三段論法的に考えると具合がよさそう、ということはあるでしょう。
文章を読んでいて、「これは定言三段論法で表してみると理解しやすいのでは？」と思えるような論理展開に出会うこともあるでしょう。
そんな時「この理屈は、形の上で正しいのかな？」とチェックできるように、今回は定言三段論法が「よい形」であるための規則を見ていきます。
その前に、前回クイズの解答です。
前回クイズ解答
問題(再掲)
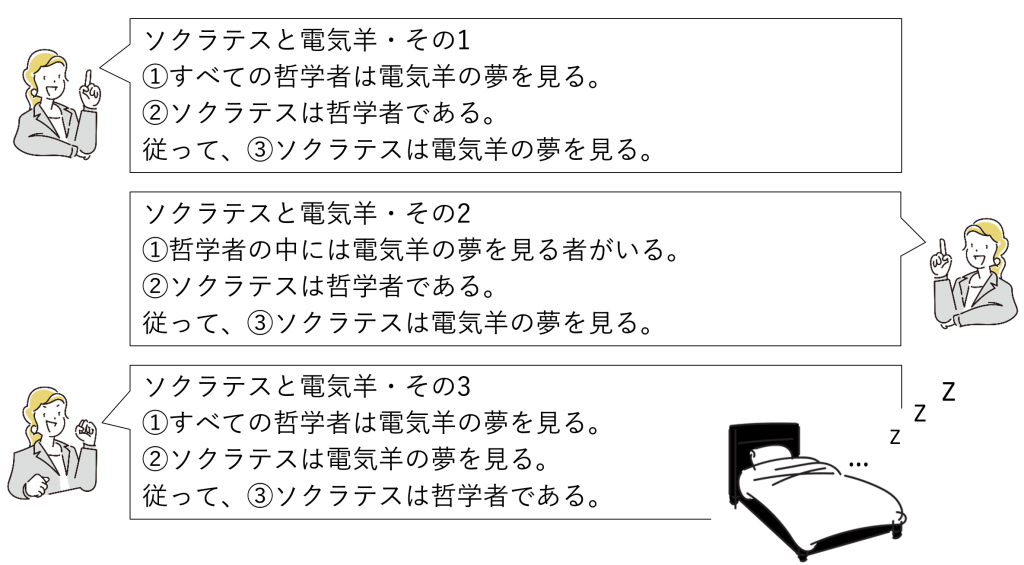
下図の「ソクラテスと電気羊」その1～3について考えてみてください。
- 小名辞S、大名辞P、媒介項Mに当たるのは何か
- 各文は全称/特称、肯定/否定どれに当たるか
解答
その1。
- 小名辞Sは「ソクラテス」、大名辞Pは「電気羊の夢を見る」、媒介項Mは「哲学者」です。
- 大前提①は「すべてのMはPである(全称肯定)」の形、小前提②は「すべてのSはMである(全称肯定)」の形、結論③は「すべてのSはPである(全称肯定)」の形です。
- （ちなみに、①M-P, ②S-M, ③S-Pですから第1格、式はAAAです）
その2。
- 小名辞S、大名辞P、媒介項Mはその1と同じです。
- 大前提①は「あるMはPである(特称肯定)」の形、小前提②は「すべてのSはMである(全称肯定)」の形、結論③は「すべてのSはPである(全称肯定)」の形です。
- （ちなみに、①M-P, ②S-M, ③S-Pの第1格、式はIAAです）
その3。
- 小名辞Sは「ソクラテス」、大名辞Pは「哲学者」、媒介項Mは「電気羊の夢を見る」です。
- 大前提①は「すべてのPはMである(全称肯定)」の形、小前提②は「すべてのSはMである(全称肯定)」の形、結論③は「すべてのSはPである(全称肯定)」の形です。
- （ちなみに、①P-M, ②S-M, ③S-Pの第2格、式はAAAです）
ソクラテスが電気羊の夢を見られるために
押さえておきたい定言三段論法の「よい形」の規則
ソクラテスと電気羊・その1は、内容(意味)から「これは前提から無理なく結論が導けるな」と思った人は多いのではないでしょうか。
その2、その3では、やはり内容(意味)を見て「この前提からこの結論は、ちょっと無理があるのでは？」「何かおかしくないか？」と、感じた人も多いのではないでしょうか。
内容や意味の面で「？」と感じる主張は、形を調べてもおかしいものです
（内容面で正しそうに見えても、形としてはよくない（妥当でない）ものもあります）。
定言三段論法的な推論の“よしあし”が、内容や意味の吟味以前に、形から読み取れることを見ていきましょう。
定言三段論法の「よい形」の規則 (1) 概念の数
登場する名辞(概念)は、三つであること
ひとつの主張(大前提、小前提、結論の組)に登場する名辞(概念)は、小名辞S、大名辞P、媒介項Mの3個に限られます。3個より多いと、意味上の混乱が生じたり、媒介する概念がなくなって論が成り立たなくなります(図7-1)。
明らかに異なる名辞(概念)が4つ以上あるのがいけないのはもちろん、言葉の意味や解釈、表現などから名辞が多過ぎる状態になってしまってもいけません。
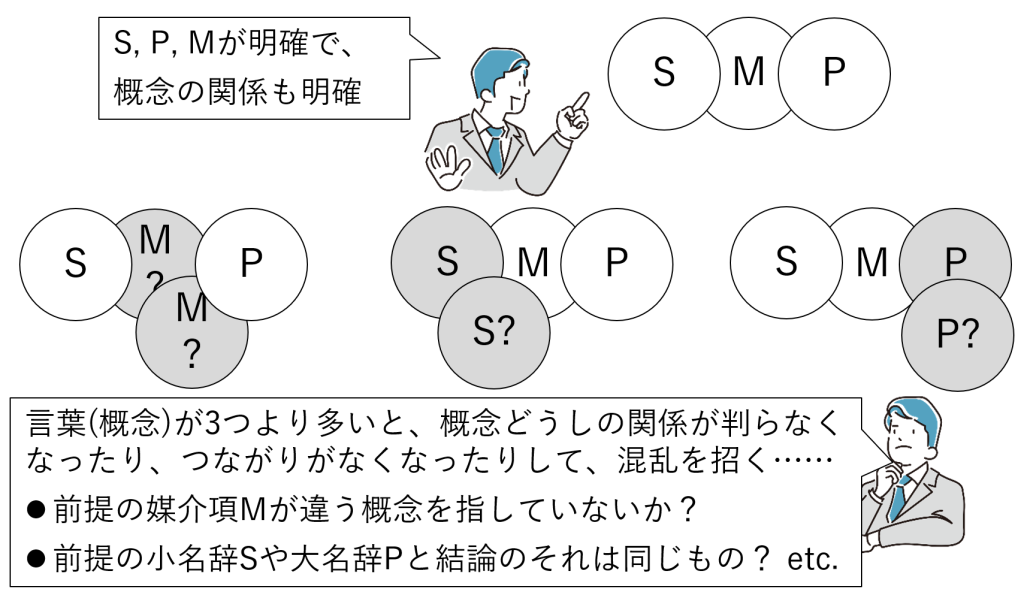
逆に登場する名辞(概念)が3個より少なく見える場合は、名辞が前提の中で省略されている可能性もあります（周知である、議論の背景として共有されている、などから省略されている事柄を補うと、正しい定言三段論法の形になる場合もある）。
そのような場合は実際の論理展開で見かけることも多いものです。主張を注意深く読み込んで「前提が隠れているのでは？」と考えてみるのがよいでしょう（ただし、本当に名辞が足りていない場合もあります）。
定言三段論法の「よい形」の規則 (2) 周延
周延とは、「その概念が当てはまるすべての対象について言われている」状態でした（「ソクラテスは電気羊の夢を見るか？(前編)」）。
周延の規則① 媒介項は必ず周延されること
媒介項Mは、前提の中で一度は周延されている必要があります。
媒介項が周延されることで、「Mに関係しているS」と「Mに関係しているP」が結びつき、結論が成り立ちます。
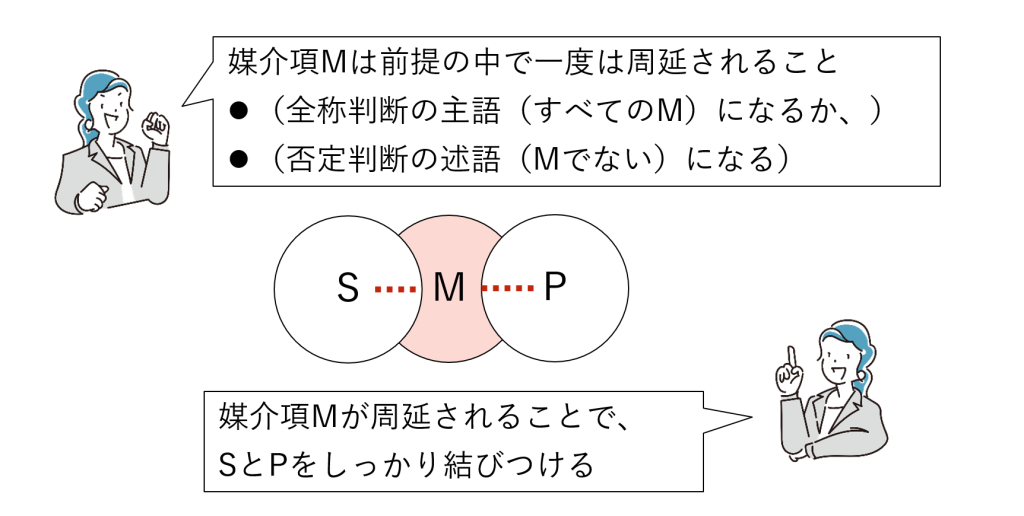
「ソクラテスと電気羊・その1」で「なるほど、ソクラテスは電気羊の夢を見るね」と判断できるのは、「哲学者」という媒介項が（「すべての」という全称により）周延され、「ソクラテス」という概念と「電気羊の夢を見る」という概念が「哲学者」を介して結びつくからです（それだけではありませんが）。
その2、その3はこの規則に反しており、媒介項「哲学者」(その2)、「電気羊の夢を見る」(その3)が周延されていません（後述「周延に関する誤謬」参照）。
周延の規則② 前提で周延されていないものは結論でも周延されないこと
小名辞、大名辞は、前提で周延されていない（不周延）なら結論でも不周延である必要があります（結論で周延されるなら、前提で周延されている必要がある）。
一部についての主張が、無条件で全体に当てはまるとは言えないからです。
なお、周延されている名辞を結論で周延しないことはできます。
定言三段論法の「よい形」の規則 (3) 肯定と否定
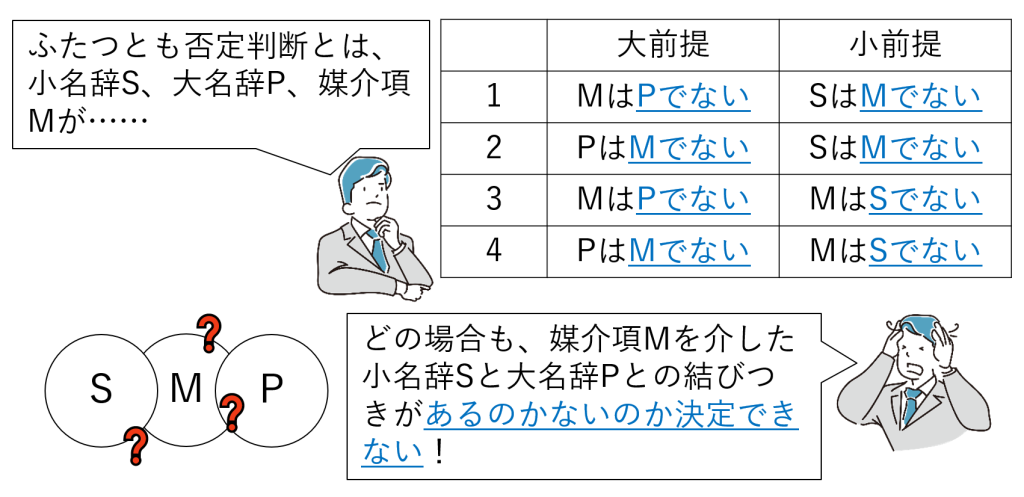
肯定と否定の規則① 前提がふたつとも否定なら、結論は出せない
前提がふたつとも否定の場合、結論は出せません。
肯定と否定の規則② 前提のどちらかが否定なら、結論は否定
前提のひとつが否定の場合、結論は否定になります。
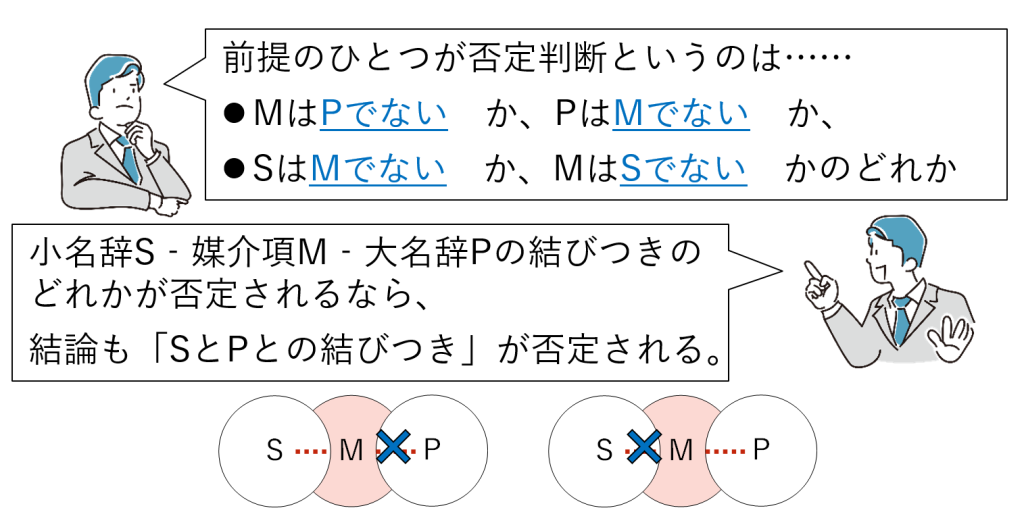
肯定と否定の規則③ 前提がどちらも肯定なら、結論は肯定
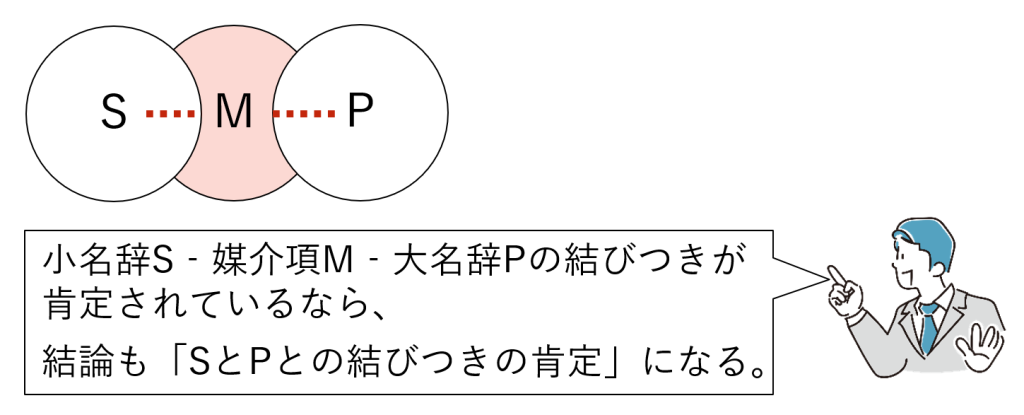
前提がふたつとも肯定の場合、結論は肯定になります。
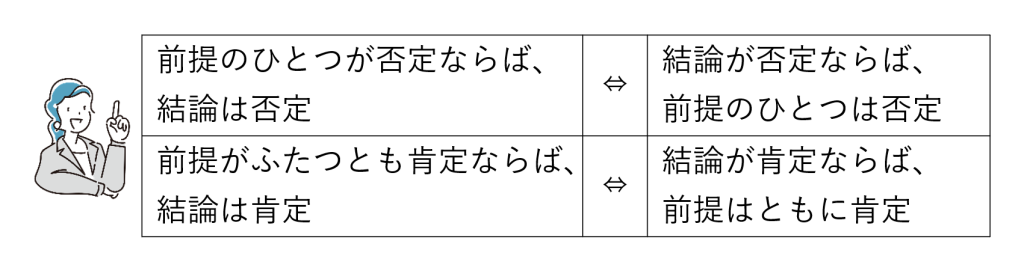
肯定と否定の規則・同値関係
肯定と否定の規則②③は、それぞれ逆も成り立ちます。(図7-7)
定言三段論法の「よい形」の規則 (4) 全称と特称
周延の規則、肯定と否定の規則から導出できる派生的な規則ですが、知っておくと便利な規則です。
全称と特称の規則① 前提がどちらも特称なら、結論は出せない
前提がふたつとも特称の場合、結論は出せません。
全称と特称の規則② 前提のどちらかが特称なら、結論は特称
前提の一方が特称の場合、結論は特称となります。
定言三段論法の「よい形」の規則 補足
ここまで挙げた「よい形」の規則はすべての格（「ソクラテスは電気羊の夢を見るか？(前編)」、図6-6）に共通で、
定言三段論法の形の“よしあし”は、これらの規則で調べることができます。
（これらの規則から派生できる規則は割愛しています。
また、これらの規則を踏まえて格ごとに格の形から来る制約があり、その結果「ひとつの格に、妥当な式は6個」となりますが、それらの説明も割愛します）
定言三段論法・気をつけたい落とし穴(誤謬)
定言三段論法の形式面で気をつけたい点は、「よい形」の規則の裏返しと言えます。
概念の数に関する誤謬
「ひとつの主張に登場する名辞(概念)は3個であること」(図7-1)に関して、名辞(概念)が3個より多くなっている誤りを四個概念の誤謬といいます。
現れている名辞(概念)の数だけでなく、以下のような点に注意しましょう。
- 使われている言葉の意味は明確か
- 多義的な言葉を使ったり、言葉の意味づけが曖昧だったりすると混乱を招く。
- 「同じ言葉は同じ意味」になっているか
- 言葉は同じでも、意味することが違っていると混乱を招く。
- 「同じ概念には同じ言葉」を使っているか
- 同じ概念を異なる言葉・表現で言い換えたり、（微妙に）違う言い回しを用いたりすると混乱を招く。
周延に関する誤謬
周延の規則①(図7-2)を守っていないことを、媒介項不周延の誤謬といいます（中名辞不周延の誤謬、媒概念不周延の誤謬ともいいます）(図7-12)。
周延の規則②(図7-3)を守っていないことを、 大名辞不当周延の誤謬、小名辞不当周延の誤謬といいます(図7-13, 図7-14)。
（こちらは「不当周延」です。媒介項の不周延とは言葉も意味も違います）
本連載最初の「論理のかたち。推論とは」で例に挙げた「イヌの三段論法」は小名辞不当周延の例になっています。（そのまま再掲していますが、大前提は②、小前提が①と並びを変えて読むと理解しやすいでしょう）
肯定と否定の規則に関する誤謬
肯定と否定の規則①(図7-4, 図-4a)に反して結論を出していることを否定前提の誤謬や否定二前提の誤謬といいます。
また、肯定と否定の規則②(図7-5, 図7-7)に反していることを不当肯定の誤謬、
肯定と否定の規則③(図7-6, 図7-7)に反していることを不当否定の誤謬
といいます。
あんがい縁がある推論の形
前回、今回と、定言三段論法の概要を紹介してきました。
修飾なしで「三段論法」というとこの形を思い浮かべる人は多いと思います（筆者もそうでした）。どのような推論の仕方をするものなのか、感触をつかめたでしょうか。
私たちが目にしたり、考えたりする中には、このような「概念どうしの関係」として表せるものごとや、そうすると考えやすいものごともあります。
「あの人はそそっかしいから、○○だ」といった主張も、「すべてのそそっかしい人は○○だ。あの人はそそっかしい。だからあの人は○○だ」といった定言三段論法の形で整理したり、考えを明確にしたりできる場合もあります。
（そうすると、「そそっかしい人はみな○○なのか？」といった、考えを批判的に見る視点も生まれやすくなります）
こういう推論の形があるということ、そしてできればその考え方を知っておくのは有益でしょう。
クイズ
ISTQB Foundaton Level V4.0シラバスの記述を元にした主張があります（()内は章節番号）。
それぞれについて、形に着目して、妥当な（よい形の）主張かどうか、今回の説明を元に考えてください。
（解答は次回に）
次回
次回、次々回は、これまで推論の形ごとに紹介してきた「気をつけたい落とし穴」について、
- 「形式面で気をつけたい落とし穴」をおさらいし、
- 「内容面で気をつけたい落とし穴」を詳しく探検
していきます。
参考文献
- 近藤洋逸, 好並英司 『論理学入門』 岩波書店 1979
- 藤野登 『論理学 伝統的形式論理学』 内田老鶴圃 1968
- 鈴木美佐子 『論理的思考の技法Ⅱ』 法学書院 2008
図版に使用した画像の出典
- Loose Drawing
- 人物画をお借りしています。
