テストエンジニアが身につけておきたいスキルの一つ「論理のスキル」。
「論理の言葉」の意味や働きに注意が向くようになったら、文や文章の読み書きで実践していきましょう。
この連載では、「論理スキル“実践編”」と題して、「文章の筋道を把握する、主張を理解する」「文や文章の筋道を組み立てる」ことに役立つ推論の形を見ていきます。
＜テストエンジニアのための論理スキル[実践編] 記事一覧＞※クリックで開きます
ここまで、基本的な推論の形を取り上げて、その考え方を解説してきました。
今回と次回は、推論を読んだり組み立てたりする際に「気をつけたい落とし穴（誤謬）」に焦点を当てます。
今回は、各回でも説明した「形式面で気をつけたい落とし穴」のおさらいです。
まず前回クイズの解答から。
前回クイズ解答
問題(再掲)
ISTQB Foundaton Level V4.0シラバスの記述を元にした主張があります（()内は章節番号）。
それぞれについて、形に着目して、妥当な（よい形の）主張かどうか、前回の説明を元に考えてください。
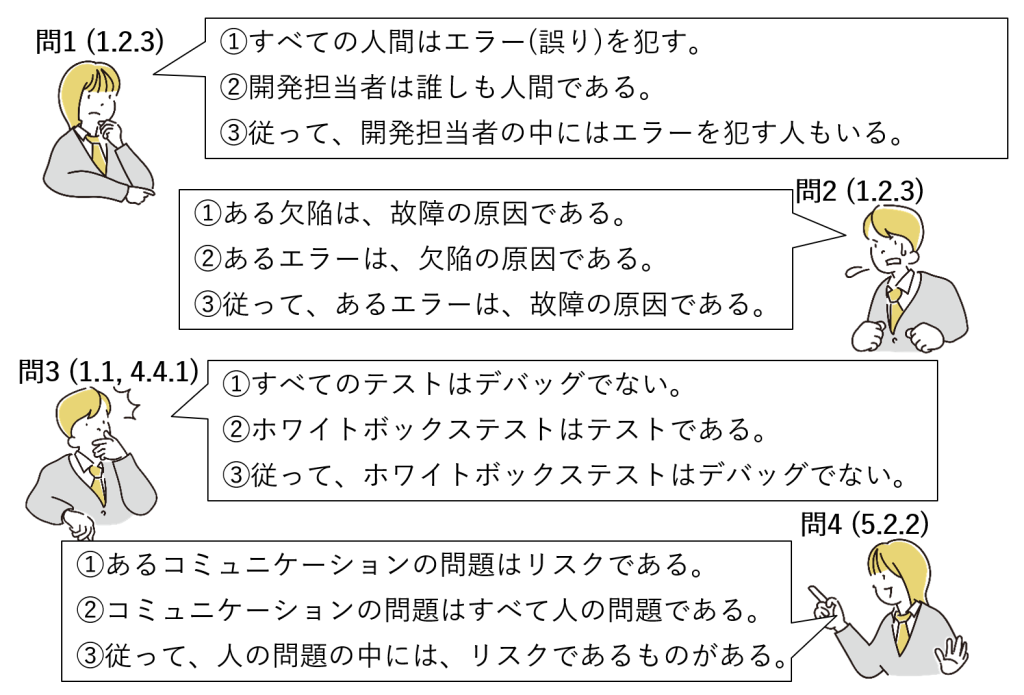
解答
問1。
- 媒介項「人間」は大前提①（全称肯定の主語）で周延されており、周延の規則①を守っています。
- 大名辞「エラーを犯す」は大前提①、結論③とも不周延。小名辞「開発者」は小前提②で全称の主語、③で特称の主語で、どちらも周延の規則②を守っています。
- ①②③いずれも肯定であり、肯定と否定の規則③を守っています。
- 以上から、妥当な形です。ちなみに第1格のAAIという式です。
問2。
- 媒介項「欠陥」が①（特称の主語）、②（肯定の述語）ともに不周延であり、周延の規則①に反しています。
また、①②とも特称文ですから、全称と特称の規則①に反しています。
この2点から、非妥当な形です。 - 一見、意味内容は正しそうに見えるかも知れませんが、媒介項が①と②で同じ概念(の範囲)を指しているかどうか不明です。
- 媒介項には別の問題もあります。
①では「欠陥」と言っているのに対し、②では「欠陥の原因」と言っています。両者は同じ概念と言えるでしょうか？ - ちなみに第1格です。式の形はIIIになります(前述の理由から、すべての格で非妥当)。
問3。
- 媒介項「テスト」は①で周延されており（全称の主語）、周延の規則①を守っています。
- 大名辞「デバッグ」は①③で周延されています（否定の述語）。
- 小名辞「ホワイトボックステスト」は②③ともに「ホワイトボックステストの全体」（全称）と解釈できます。
- 大前提①が否定、結論③が否定で、肯定と否定の規則②を守っています。
- 以上から、妥当な形です。ちなみに第1格のEAEという式です。
問4。
- 媒介項「コミュニケーションの問題」は②で周延されており（全称の主語）、周延の規則①を守っています。
- 大名辞「リスク」は①③ともに不周延、小名辞「人の問題」は②③ともに不周延で、どちらも周延の規則②を守っています。
- ①②③いずれも肯定であり、肯定と否定の規則③を守っています。
- 以上から、妥当な形です。ちなみに第3格のIAIという式です。
推論の形式で気をつけたい落とし穴
各回で説明してきた推論形式には、形式面で気をつけたい落とし穴(誤謬：ごびゅう)があります。
今回、復習を兼ねて一覧できるようにしました。
これらは、その推論形式の性質から意味内容の真偽とは関係なく「これは間違った推論」と言えてしまう誤りです。
いくら内容面では正しいと思えるとしても、形の上で問題があるものは筋道を損ねてしまっており、よい主張とは言えません。
“または”で気をつけたい落とし穴
“または”は包含的
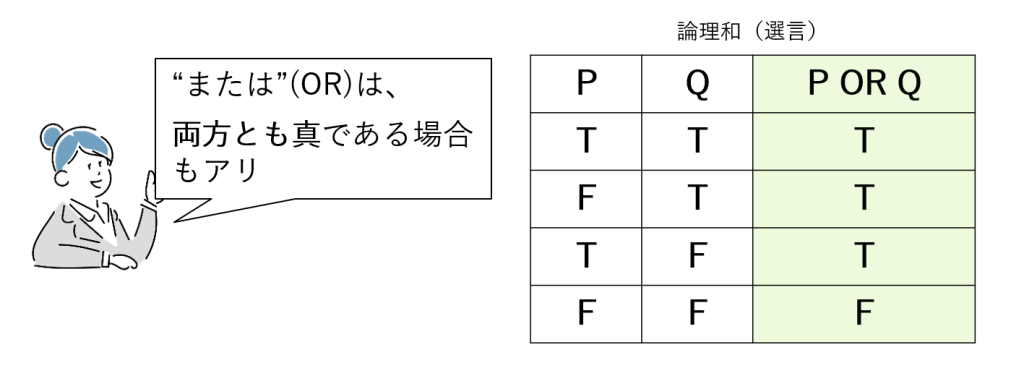
論理の言葉としての“または”（選言。“入門編”では論理和(OR)として紹介)は、「PとQがともに真でも成り立つ」という性質を持っています。
参照
・論理スキル[再]入門 [第3回] プログラムレベルのロジック(2)解説編・基本の論理演算
・論理スキル[実践編]“または”を使って推論する
この特徴から 包含的選言 などとも呼ばれます。
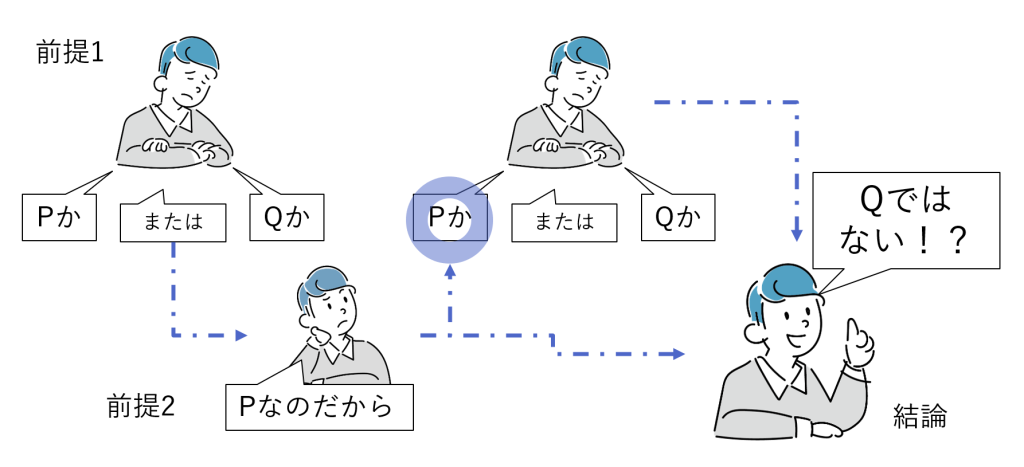
選言三段論法での誤謬
この性質から、選言肢の一方が真だからといって、他方が偽であるとは言えません。図8-2は誤りです（PとQを入れ換えても同じ）。
（選言三段論法の回では“タイプB”という本連載独自の呼称を使っています）
（排他的な“または”なら誤りではないが）
日本語だと同じ“または”という語になりますが、
「P, Qどちらかが真だが、ともに真ということはない」「Pが真であるか(その場合Qは偽)、または、Qが真(その場合Pは偽)」
という場合を表す“または”があります。
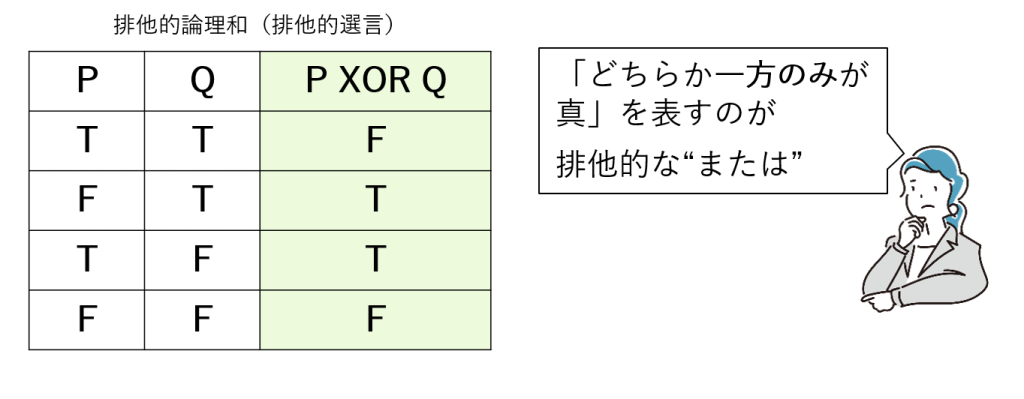
これは“排他的選言”や“排他的論理和(Exclusive OR, XOR)”などと呼ばれます(図8-3)。
この意味の“または”である場合は、図8-2の形は正しくなります。
（どちらでも正しいのはこちらの形）
選言三段論法で、包含的選言でも排他的選言でも正しいのは、選言肢の一方を否定し、残る選言肢を結論とする形です（図8-4。PとQを入れ換えても同じ）。
（選言三段論法の回では“タイプA”という本連載独自の呼称を使っています）
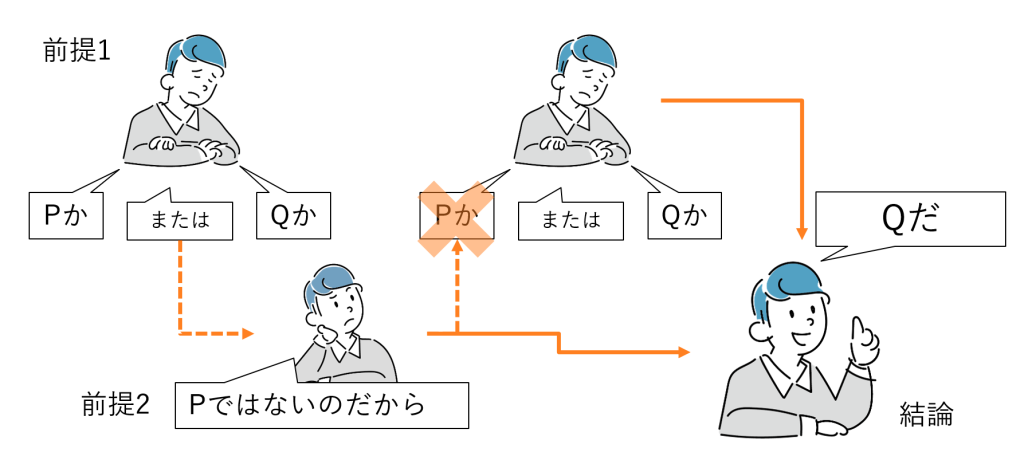
どちらの意味で使われているか、どちらに該当するのか、に気をつける
残念ながら、私たちが日ごろ使う言語では、どちらの選言かによって異なる言葉を使い分けるようにはなっていません。
文や主張の中に“または”が現れた場合は、どちらの意味なのかを選言肢の内容や文脈から判断する必要があります。
例。
ヨーロッパ向けの製品を担当するには、フランス語の知識か、またはドイツ語の知識が必要です。
フランス語の知識とドイツ語の知識を両方持っていても仕事の妨げにはならないでしょうから、この“または”は包含的な選言と解釈できます。
- 【非妥当】「担当しているミオさんはドイツ語ができるから、フランス語はできないかもね」
- 【妥当】「担当しているエマさんはドイツ語はできないそうだから、フランス語に堪能ということなんだろう」
両方の知識を持っている人は担当できないという条件がつくなら、【非妥当】の方も正しくなります（が、そういう条件にしている理由が気になりますよね……）。
例。
ハルトさんは、エマさんか、または、ミオさんのどちらかと結婚するだろう。
重婚を認めていない国/地域であれば、この“または”は排他的選言と解釈するのが自然でしょう。
- 【妥当】「ハルトさんはミオさんと結婚する。だから、ハルトさんはエマさんとは結婚しない」
“ならば”で気をつけたい落とし穴
“ならば”と逆・裏・対偶（何度でも確認しましょう）
条件法“ならば”と逆・裏・対偶のうち、
「PならばQ」が正しい(真である)時に正しいと言えるのは対偶「QでないならばPでない」のみです。
参照
・論理スキル[再]入門[第6回] 文レベルのロジック (2)条件・場合を表す言葉
仮言三段論法での誤謬――前件否定と後件肯定
混合仮言三段論法で、
「①PならばQ。②Q。③従って、P」は「PならばQ」の「逆」を、
「①PならばQ。②Pではない。③従って、Qではない」は「PならばQ」の「裏」を、それぞれ言っていることになります。
（前者が後件肯定の誤り、後者が前件否定の誤り）
これは誰しもうっかり間違えてしまいがちな、陥りやすい「落とし穴」です。
森高千里というミュージシャン/シンガーのヒット曲に次の一節があります（発表は30年ほど前）。
私がオバさんになったら あなたはオジさんよ
「私がオバさんになっても」作詞・森高千里
森高千里さんが2024年夏のライブ(野外フェス)に出演した際の写真が先日ネットに公開されたそうですが、往時から全然変わらぬお姿とか。
（参考：別サイト(J-CASTニュース)の記事）
その姿とこの歌詞から、
①森高千里がオバさんになったならば、我々はオジさんである。
②だが、森高千里はオバサンになっていない！
③従って、我々はオジさんではない！！
という推論が成り立つ！ のでは！！ ……と考えたくなりますが、残念ながらこれは前件否定です。
直感や願望、見た目のインパクトなどから、つい「わかりやすい」推論に飛びついてしまうというのは、ありがちなことです。
（論理的には、そして現実にも、森高千里さんがオバさんにならないからといって、男子がオジさんにならないとは限らないわけです）
（ただし、逆と裏が成り立つ場合はある）
“ならば”が、「PならばQ」と同時に「QならばP」を主張する等値(同値)の“ならば”（双条件法）であるならば、元の主張が正しい時に逆や裏も正しくなります。
参照
・論理スキル[再]入門[第6回] 文レベルのロジック (2)条件・場合を表す言葉
・論理スキル[実践編]基本的な推論形式
双条件法の例①。
ある数Xが1より大きい自然数で、かつ1と自分自身を除き約数を持たない時、そしてその場合に限り、Xを素数という。
用語や概念の定義では双条件法は重要な役割を果たします。なぜだと思いますか？
双条件法の例②。
志望者がフランス語か、またはドイツ語の知識を持っている場合、そしてその場合に限って、ヨーロッパ向けの製品を担当することができる。
条件法の“ならば”の場合に対して、「ヨーロッパ向けの製品を担当できる条件」はどう違うでしょうか？
“ならば”の前後に気をつける
等値の“ならば”はそれと分かる言い回しなしに使われることもありますから、なおさら、前件と後件の意味内容とつながりには注意を払いましょう。
例。
「あの科目は、テストの結果が悪かったら単位は取れない。単位が取れなかったということは、テストの結果が悪かったんだ」
テストの得点だけが単位取得の評価項目なら、この“ならば”は等値(同値)の“ならば”であり、推論は正しいと言えます（例文では情報がないので、正しいと断言するのは早計です）。
他にも評価項目があるなら（出席回数/出席率など）、この推論は後件肯定の誤りです。
例。
「もしあなたがこの手紙を読んでいるなら、私は既に死んでいるということだ」
小説、映画、ドラマなどでしばしばお目にかかる場面ですが、
「あなた」がその手紙を読んだのに「私」が生きているということはなく、「私」が死んだ時のみ「あなた」の目に触れるのでしょうから、これは等値(同値)の“ならば”、双条件法と考えてよいでしょう（なので、ミステリーやスリラーでは、実は死んでおらず……という展開が活きるわけでしょうね）。
両刀論法でも気をつける
両刀論法も“ならば”を用いた推論ですから、前件否定や後件肯定には気をつけましょう。
定言三段論法で気をつけたい落とし穴
前回取り上げた形ですが、おさらいしましょう。
四個概念の誤謬以外は、形から判断がつきます。
概念の数に関する誤謬
定言三段論法に4個(以上)の概念が登場してしまうと（四個概念の誤謬。媒概念曖昧の誤謬などともいいます）、概念(名辞)どうしの関係がつけられず、正しい推論ができなくなります。
特に次のような場合に気をつけましょう。
- 使われている言葉の意味は明確か
- 「同じ言葉を同じ意味」で使っているか（文によって違った意味に解釈できることはないか）
- 「同じ概念には同じ言葉」を使っているか（文によって違った概念を指していると解釈できることはないか）
（言葉の意味や使い方が揺らいでいないか、というのは、定言三段論法に限らず気をつけたいことでもあります）
周延に関する誤謬
媒介項Mが特称(主語の場合)か、または肯定(述語の場合)でしか現れていないなら、媒介項不周延の誤謬（周延の規則①の違反）です。
大名辞不当周延の誤謬、小名辞不当周延の誤謬（周延の規則②の違反）は、それぞれの名辞(概念)の全称/特称、肯定/否定に注意しましょう。
肯定と否定の規則に関する誤謬
否定二前提の誤謬 (肯定と否定の規則①の違反)、不当肯定の誤謬 (同②の違反)、不当否定の誤謬 (同③の違反)は、全体の形を見ましょう。
次回
次回は、演繹的な推論に限らず、考えを組み立てたり述べたりする際に意味内容の面で「気をつけたい落とし穴」を取り上げます。
これまでで取り上げていない“落とし穴”がたくさん出てきます。お楽しみに。
参考文献
- John Nolt, Dennis Rohatyn(著), 加地大介(訳) 『現代論理学 (Ⅰ)』 オーム社 1995
- レイモンド・スマリヤン(著), 高橋昌一郎(監訳), 川辺治之(訳) 『記号論理学 一般化と記号化』 丸善出版 2013
- 鈴木美佐子 『論理的思考の技法Ⅰ〔第2版〕』法学書院 2013
- 弓削隆一, 佐々木昭則 『例解・論理学入門』 ミネルヴァ書房 2009
- 近藤洋逸, 好並英司 『論理学入門』 岩波書店 1979
- 藤野登 『論理学 伝統的形式論理学』 内田老鶴圃 1968
- 鈴木美佐子 『論理的思考の技法Ⅱ』 法学書院 2008
図版に使用した画像の出典
- Loose Drawing
- 人物画をお借りしています。
