テストエンジニアが身につけておきたいスキルの一つ「論理のスキル」。
「論理の言葉」の意味や働きに注意が向くようになったら、文や文章の読み書きで実践していきましょう。
この連載では、「論理スキル“実践編”」と題して、「文章の筋道を把握する、主張を理解する」「文や文章の筋道を組み立てる」ことに役立つ 推論の形 を見ていきます。
＜テストエンジニアのための論理スキル[実践編] 記事一覧＞※クリックで開きます
今回のテーマは、論理の言葉のうち“または”を用いる推論の形式です。
前回のクイズ解答
問題(再掲)
解答
bの条件は「aに該当せず、かつ、b独自の条件に該当する」＝「aの否定、かつ、b」ですから(図3-1の上)：
- aの条件の否定(③)： NOT(S1 >= 85 AND S2 >= 70)
- ⇒ (S1 < 85 OR S2 < 70) (ド・モルガンの法則)
- b独自の条件(⑥)と“かつ”で結ばれ：
- (S1 < 85 OR S2 < 70) AND (S1 >= 85 OR S2 >= 70) (⑦)
cの条件は「a, bいずれにも該当しない」＝「aの否定、かつ、b独自の条件の否定」ですから(図3-1の下)：
- aの条件の否定(③)： (S1 < 85 OR S2 < 70)
- b独自の条件の否定(⑥)： NOT(S1 >= 85 OR S2 >= 70)
- ⇒ (S1 < 85 AND S2 < 70) （ド・モルガンの法則）
- ③と⑥が“かつ”で結ばれ：
- (S1 < 85 OR S2 < 70) AND (S1 < 85 AND S2 < 70) (⑦)
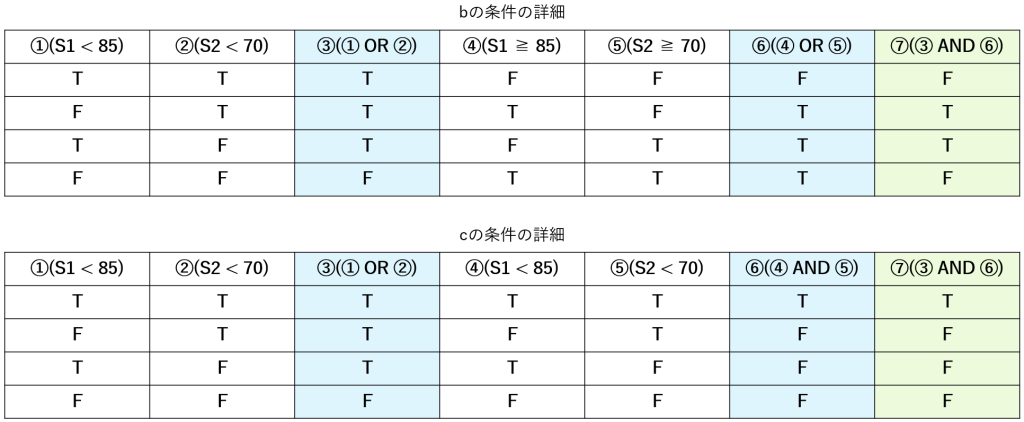
「該当しない場合」や「そうでなければ」は、プログラムならelseの一言で済みますが、このように敢えて詳細な条件を展開してみることも論理のスキルの向上につながります。
「S1の値が85未満」と「S1の値が85以上」とが同居していて両立するの？ 何か間違ったかな？ と思う人は、図3-1で“両立”することを確認してください。
“または”の意味/働きと推論
前提の“または”から結論を導く
論理の言葉“または”の意味・働きをそのまま活かして、
「Aであるか、またはBである」という前提から結論を導く推論の形があります。
前提1が選言文（“または”を用いた主張）である三段論法を「選言三段論法」といいます。前提2には、前提1から結論を導くための断言文を置きます。
選言三段論法の形式
“タイプA”
選言三段論法の基本的な形は次の通りです（本記事独自の呼称として、 “タイプA” と呼びます）(図3-3)。
①Pであるか、または、Qである。
②Pではない。
③従って、Qである。
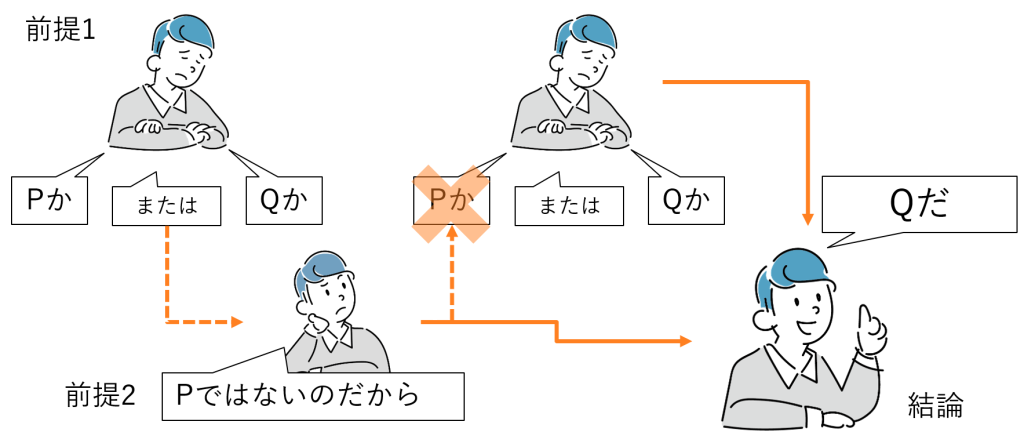
“または”(選言)がつなぐ文や語句のことを「選言肢」といいますが、
ふたつの選言肢のうちひとつが否定されれば、残る選言肢が結論になります。
（なお、PとQのどちらを否定しても同じです）
例：
①このエラーコードが出るのは、アクセス制御に問題がある場合か、データに不整合がある場合だ。
②データには不整合が発見されなかった。
だから、③アクセス制御に問題があると見てよさそうだ。
“タイプB”
次の形は、基本的に妥当ではありません（本記事独自の呼称として、 “タイプB” と呼びます）(図3-4)。
①Pであるか、または、Qである。
②Pである。
③従って、Qではない。
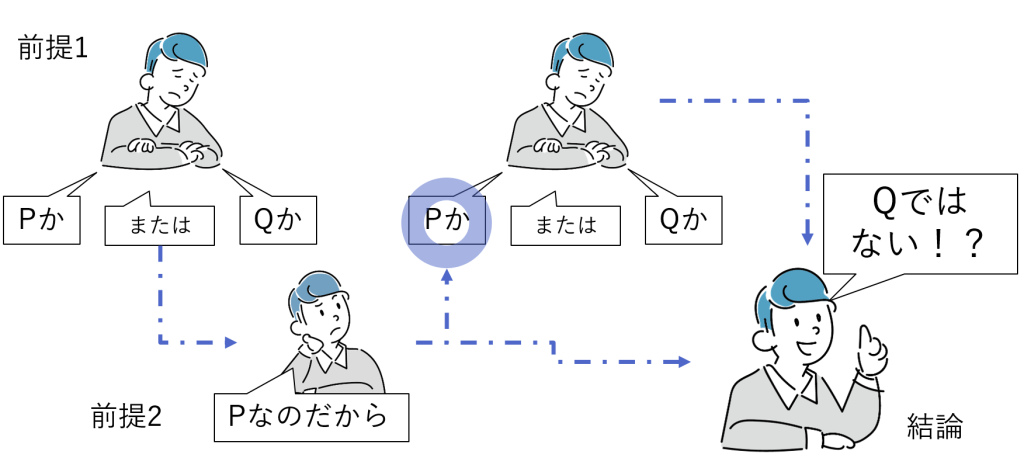
論理の言葉としての“または”は 包含的 であることに注意してください（P、Qがともに真の場合もあり得る）。
選言肢の一方が真だからといって、他方が偽であることにはなりません。
（PとQのどちらを肯定しても同じです）
例：
①このエラーコードが出るのは、アクセス制御に問題がある場合か、データに不整合がある場合だ。
②データに不整合が見つかった。
ということは、③アクセス制御には問題はないだろう。
アクセス制御の欠陥とデータの不整合は同時に起こり得るでしょうから、これは妥当な推論ではありません。
「論理のかたち。推論とは」の「ネコにはしっぽがあるか、にゃあと鳴く」の例も同じ形になっています。
選言三段論法 補足
排他的選言の場合
ただし、“または”は排他的な意味で使われることがあります（「“入門編”第5回 文レベルのロジック (1)」）。
排他的な“または”の場合には、“タイプB”も妥当 になります(図3-5)。
どちらの“または”なのか、主張の内容から判別する必要があります。
（なお、“タイプA”はどちらの“または”でも妥当 です）
例：
①この現象が起こるのは、データがゼロ件の場合か、データ件数が上限に達している場合ですね。
②調べたらデータ件数が上限いっぱいでした。
だから、このトラブルは③データがゼロ件の場合の処理は関係ないと見てよいでしょう。
選言肢が三つ以上でも成り立つ
選言三段論法は前提1が三つ以上の選言でも成り立ちます。
その場合、結論は「前提1から、前提2で否定されたものを除いた選言判断」になります(図3-6)。
選言三段論法 featuring ド・モルガンの法則
連言の否定（「PかつQ、ではない」）から結論を導く、選言三段論法の変形のような形もあります。
①「Pであり、かつ、Qである」ということはない。
②Pである。
従って、③Qではない。
「連言の否定は、否定の選言」ですから、ド・モルガンの法則を適用して①を①’に置き換えると、
①’Pではないか、または、Qではない。
②Pである。
従って、③Qではない。
となります(図3-7)。
この場合、②が一見非妥当な形（“タイプB”）のように見えますが、これは前提1が否定であり、その否定（＝二重否定）だから「Pである」という形になっているものです。
（「①Pではないか、または、Qではない。②Pではない。従って、③Q」は、妥当ではありません）
選言三段論法・気をつけたい落とし穴(誤謬)
“タイプB”の形になっているが、前提1が「排他的な選言」でない
繰り返しになりますが、“タイプB”は排他的な“または”でなければ妥当な形ではありません。
“タイプB”の形の論理に出会った場合は、使われている“または”が排他的な意味で使われているのかどうか注意を向けてみましょう。
選言肢不完全の誤謬
「AかBかどちらか」から結論を導くわけですから、前提1で提示される選言肢が主張したい事柄の範囲をカバーできていないと、誤った結論を導いてしまう惧れがあります。
これを「選言肢不完全の誤謬」といいます(図3-8)。
そもそも、選言肢が不適切
選言肢不完全の誤謬に通じますが、“または”でつなぐのが適当ではないものを選言肢に掲げるのも、前提の正しさを損ねる惧れがあります。
- 極端な場合を取り上げている（詳細を無視するなど）
- 関連が薄いか、ないものを選言肢にしている
- ありうる様々な場合を見落としている
- etc.
クイズ
（解答は次回に）
※問題の図版に誤りがございました（問3が間違っています）。
ご覧になった方を混乱させたことをお詫び申し上げます。
以下に正しい図を掲載します。
次回
「基本的な推論形式」で挙げたうち、「“ならば”を使う推論の形（仮言三段論法）」を取り上げます。
参考文献
- 近藤洋逸, 好並英司 『論理学入門』 岩波書店 1979
- 藤野登 『論理学 伝統的形式論理学』 内田老鶴圃 1968
- John Nolt, Dennis Rohatyn(著), 加地大介(訳) 『現代論理学 (Ⅰ)』 オーム社 1995
- レイモンド・スマリヤン(著), 高橋昌一郎(監訳), 川辺治之(訳) 『記号論理学 一般化と記号化』 丸善出版 2013
図版に使用した画像の出典
- Loose Drawing
- 人物画をお借りしています。
